CATEGORY
統計
統計学入門
統計を学びたい方に向けた解説記事をまとめています。
数式や専門用語を極力廃止して『統計学とは何か?』という疑問に答えながら、統計学の使い方やデータに騙されない手法を公開していきます。
目安:統計検定 3級
初級者の統計学
統計を使いたい方に向けた解説記事をまとめています。
統計学の基礎をしっかりと理解しながら、なんとなく使っているレベルから脱却することを目的とした記事を公開していきます。
目安:統計検定 2級 ~ 準1級
中級者の統計学
統計を日常的に使う方に向けた解説記事をまとめています。
基本的に全ての項目で証明を行い、必要に応じて辞書のように扱える記事を公開しています。
目安:統計検定 準1級 ~ 1級
コラム
気になった出来事や思い付いた内容を記事にまとめて公開しています。
- 2025年2月22日
相対的リスクとオッズ比
リスクとオッズ リスクとオッズは、それぞれ『全体に占める割合』と『成功と失敗の比率』を表しています。例えば、総勢100名にアンケートを行い、60名がYES、40名がNOと答えたとしましょう。 相対的リスクとオッズ比 Point 調査対象 コントロール群 合計 状態A \(T_A\) \(C_A\) […]
- 2025年2月22日
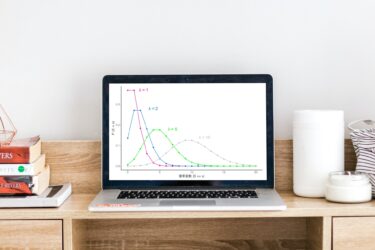
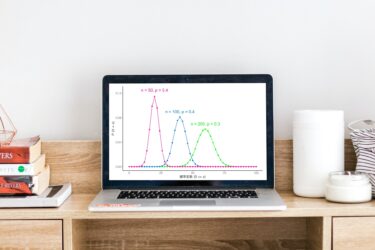
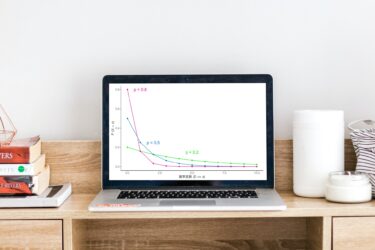
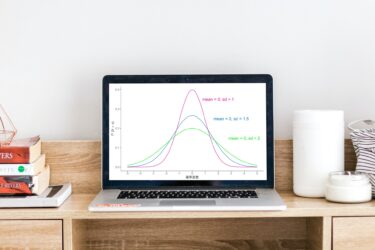
『確率分布とは何か?』に2分で答える
確率分布とは何か 確率分布とは 『確率変数とは何か?』では『データの本質』を確率変数と定義しました。この時、確率分布を以下の通り定義しましょう。 定義 『確率変数の種類と特徴』 正確には確率分布自体を種類、確率分布が持つ母数を特徴と表します。 具体例 全ての確率変数は『確率分布 × 母数』の組み合わ […]