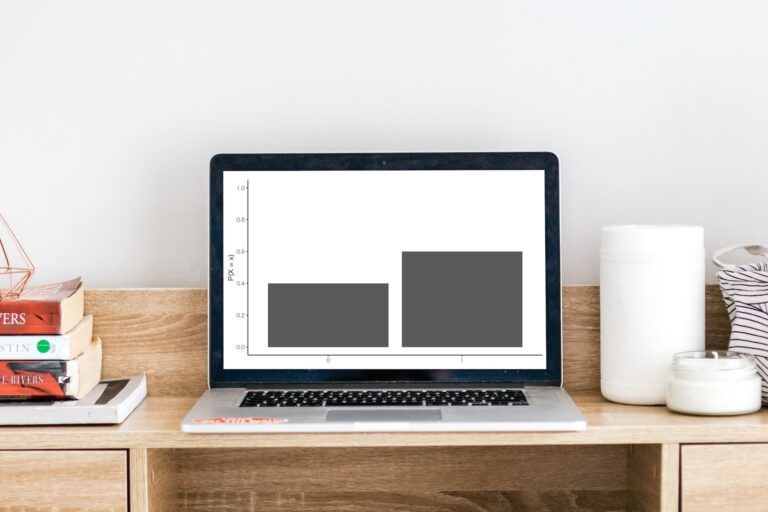
ベルヌーイ分布とは
成功(1)と失敗(0)のどちらかの値を取る離散型の確率分布になります。
成功確率をpで表し、ベルヌーイ分布に従う試行をベルヌーイ試行と呼びます。
具体的な事象
- 50%の確率で表が出るコインでコイントスを行う
⇨ 成功: 表が出る 失敗: 裏が出る - 1/6の確率で1の目が出るサイコロを振る
⇨ 成功: 1の目が出る 失敗: 1以外の目が出る - 2%の確率でクリックされる広告を表示する
⇨ 成功: クリックされる 失敗: クリックされない
確率分布
\begin{align}
X \sim Be(p)
\end{align}
ベルヌーイ分布の確率変数と母数は以下の意味を持ちます。
なお、ここではベルヌーイ分布を\(Be(p)\)と表します。
- X: 成功(1)か失敗(0)のどちらかを表す
- p: ベルヌーイ試行が成功する確率
確率質量関数
\begin{align}
P(X=x)=p^x(1-p)^{1-x}
\end{align}
ベルヌーイ分布の確率質量関数は以下の要素から構成されます。
- 成功する確率 \(\longrightarrow p^x\)
- 失敗する確率 \(\longrightarrow (1-p)^{1-x}\)
「成功する確率」と「失敗する確率」
成功する確率を\(p=0.6\)とした時
- 成功: (\(x=1) \rightarrow 0.6^1 \cdot 0.4^0 = 0.6\)
- 失敗: (\(x=0) \rightarrow 0.6^0 \cdot 0.4^1 = 0.4\)
性質
期待値
\begin{align}
E[X]&=p \\
\end{align}
分散
\begin{align}
V[X]&=p(1-p)
\end{align}
関係する分布
二項分布
ベルヌーイ分布を多試行化したものが、二項分布になります。
なお、ここでは二項分布を\(B(n,p)\)と表します。
\begin{align}
Be(p) \longrightarrow B(1, p)
\end{align}
証明
期待値
\begin{align}
E[X] &= \sum_{x=0}^{1} x P(X=x) \\
&= \sum_{x=0}^{1} x p^x(1-p)^{1-x} \\
&= 0p^0(1-p)^{1-0}+1p^1(1-p)^{1-1} \\
\\
&= p \\
\end{align}
分散
\begin{align}
E[X^2] &= \sum_{x=0}^{1} x^2 P(X=x) \\
&= \sum_{x=0}^{1} x^2 p^x(1-p)^{1-x} \\
&= 0^2p^0(1-p)^{1-0}+1^2p^1(1-p)^{1-1} \\
\\
&= p \\
\\
\\
V[X] &= E[X^2]-E[X]^2 \\
\\
&= p-p^2 \\
\\
&= p(1-p) \\
\end{align}