ブラウン運動とは
ブラウン運動とは、連続でランダムに動く物体を表現する確率過程モデルになります。
具体例
- 酔っ払った親父の千鳥足
⇨ 右にふらふら、左にふらふらと動きながら進んだ道筋(ランダムウォーク) - 水中で水を吸って破裂した花粉の素粒子
⇨ 素粒子が水中を彷徨う道筋
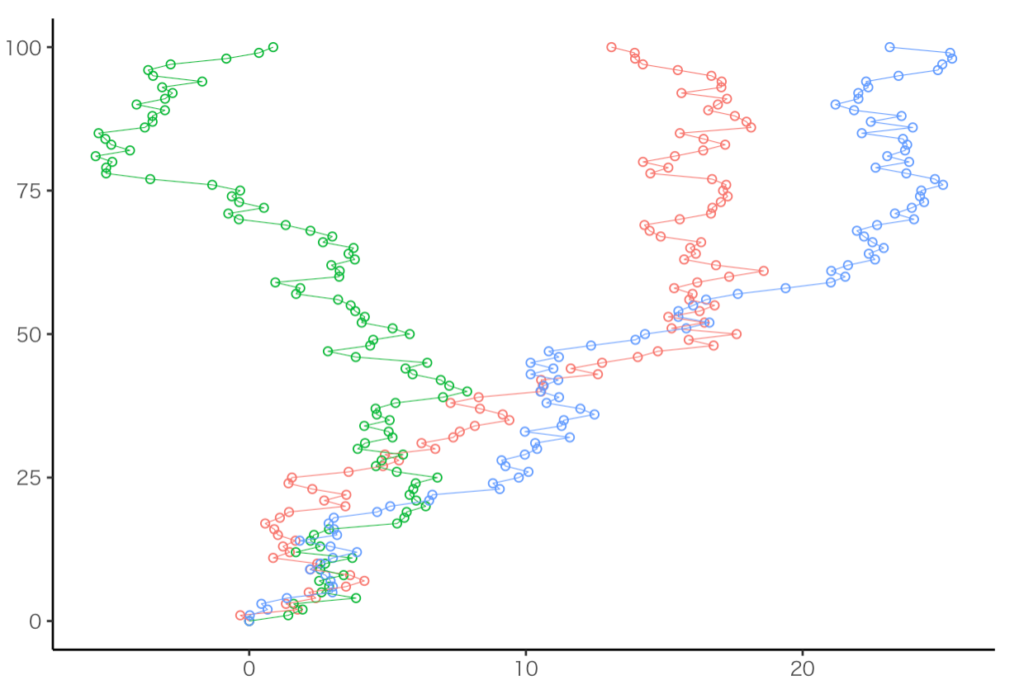
グラフ
具体例:3人の親父の千鳥足
定義
\(t(0 \leq t)\)を基準からの経過時刻、\(t=0\)を基準時刻と置きます。
この時、\(t\)だけ経過した時の現在位置を\(B_t\)と表します。
1. 経過位置\(B_t\)は正規分布に従う
式1
\begin{align}
B_t \sim N(0, \sigma^2t)
\end{align}
式1では正規分布を\(N(0, \sigma^2t)\), 定数を\(\sigma^2\)で表しています。
なお、\(\sigma^2=1\)のモデルを標準ブラウン運動と呼びます。
2. 基準位置\(B_0\)は0になる
式2
\begin{align}
&B_0=0 \\
&B_0 \sim N(0, \sigma^20)
\end{align}
基準時刻\(t=0\)の時は、平均0, 分散0の正規分布に従います。
3. 定常増分性を持つ
式3
\begin{align}
&B_b-B_a \sim N(0, \sigma^2(b-a)) \longleftarrow 0 \leq a \leq b \\
&B_t-B_0 \sim N(0, \sigma^2t)
\end{align}
終了位置\(B_b\)と開始位置\(B_a\)の差は、平均0, 分散\(\sigma^2(b-a)\)の正規分布に従います。
また、現在位置\(B_t\)も『現在位置\(B_t\)と基準位置\(B_0\)の差』と表現できます。
4. 独立増分性を持つ
式4
\begin{align}
B_b-B_a \perp B_{b’}-B_{a’} \longleftarrow 0<a<b<a'<b’
\end{align}
独立増分性とは、区間が重ならない箇所の変化量が独立であることを表します。
\(0 \leq a \leq b \leq a^{\prime} \leq b^{\prime}\)のとき、\(B_b-B_a\)と\(B_{b^{\prime}}-B_{a^{\prime}}\)は独立になります。