正規分布
| 確率分布 | \(X \sim N(\mu, \sigma^2)\) |
| 母数 | \(\mu\) \((\in \mathbb{R})\) \(\sigma^2\) \((\geq 0)\) |
| 台 | \(\mathbb{R}\) \((-\infty < X < \infty)\) |
| 確率密度関数 | \(\frac{1}{\sqrt{2\pi\sigma^2}}exp\left(-\frac{(x-\mu)^2}{2\sigma^2}\right)\) |
| 期待値 | \(\mu\) |
| 分散 | \(\sigma^2\) |
| モーメント母関数 | \(exp\left(\mu t+\frac{\sigma^2t^2}{2}\right)\) |
概要
正規分布は『連続モデル × ガウス関数』から成り立つ確率分布です。
母数に平均\(\mu\)と分散\(\sigma^2\)を持ち、主に誤差を表現する用途で利用します。
具体例
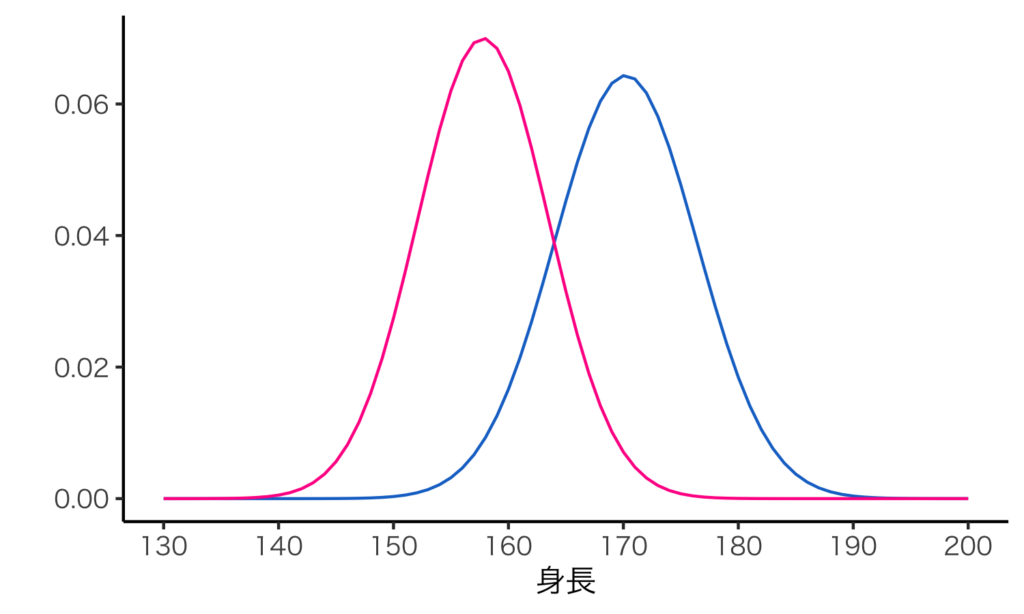
ある年の高校3年生の身長(事象が正規分布に従う例)
- 男子: 平均170.2cm, 分散\(6.2^2\)cm
- 女子: 平均157.8cm, 分散\(5.7^2\)cm
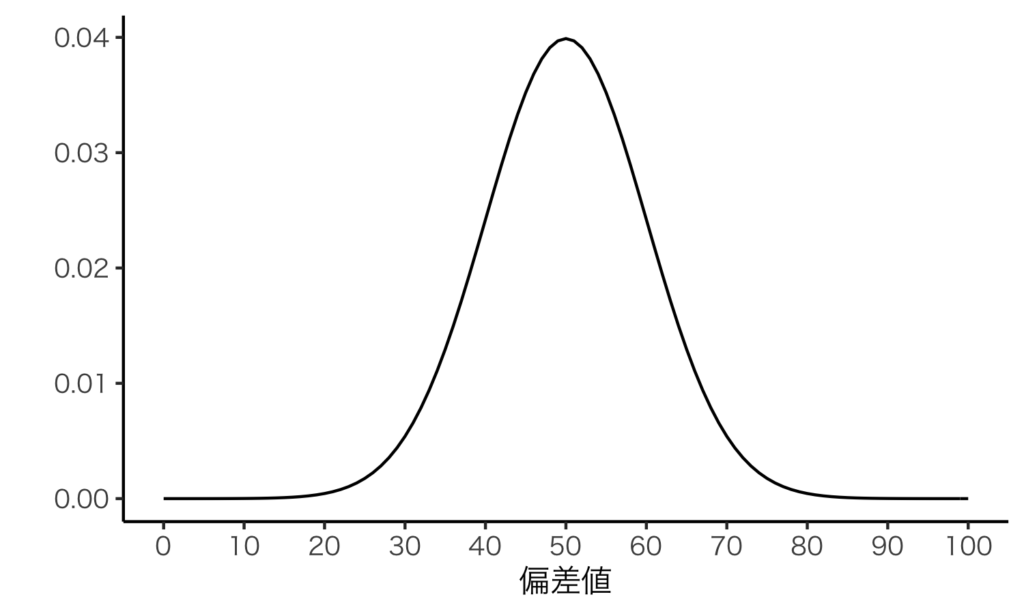
偏差値(事象が正規分布に従うと仮定した例)
- 平均50, 分散\(10^2\)
確率密度関数
式1
\begin{align}
f(x)=\frac{1}{\sqrt{2\pi\sigma^2}}exp\left(-\frac{(x-\mu)^2}{2\sigma^2}\right)
\end{align}
正規分布の確率密度関数は以下の要素から構成されます。
- ガウス関数
- ガウス関数に従属する関数
ガウス関数
ガウス関数とは、ある値に近い値ほど頻繁に発生し、遠い値ほど稀にしか発生しない性質を持ちます。また、値の出現率はある値を中心に左右対称であることが特徴です。
最もシンプルなガウス関数は \(y=exp(-x^2)\) と表現されます。
この場合のある値は0になります。
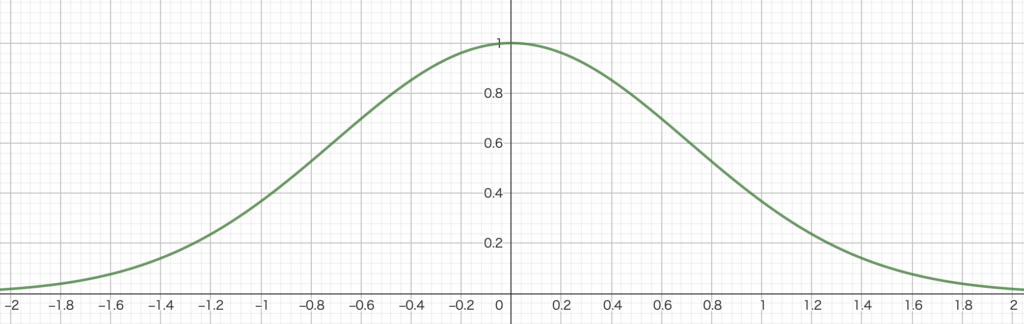
上のグラフを見て、ガウス関数と正規分布の形状が一致することに気が付くと思います。
先に結論を言うと、正規分布の正体はガウス関数になります。
平均と分散の指定
最もシンプルなガウス関数は平均が0、分散が1に固定されています。
平均と分散を可変にするためには以下のガウス関数を用います。
式2
\begin{align}
y=exp\left(-\frac{(x-\mu)^2}{\sigma^2}\right)
\end{align}
ガウス積分
ガウス関数を広義積分したものをガウス積分と呼びます。
最もシンプルなガウス関数を広義積分した結果は\(\sqrt{\pi}\)になります。
式3
\begin{align}
\int_{-\infty}^{\infty} exp\left(-x^2\right) dx=\sqrt{\pi}
\end{align}
同様に式2をガウス積分した結果は以下の通りです。
式4
\begin{align}
\int_{-\infty}^{\infty} exp\left(-\frac{(x-\mu)^2}{\sigma^2}\right) dx=\sqrt{\pi\sigma^2}
\end{align}
確率分布の条件
連続モデルの確率分布は広義積分の結果が必ず1になる性質を持ちます。
そのため、式4を確率分布として扱うために以下の形に変形します。
式5
\begin{align}
\int_{-\infty}^{\infty} \frac{1}{\sqrt{\pi\sigma^2}} \cdot exp\left(-\frac{(x-\mu)^2}{\sigma^2}\right) dx=1
\end{align}
分散の係数
正規分布の確率密度関数は慣例として式1を使用します。
勉強不足のため分散の係数に2が付与される理由は分かりませんが、式1と式5は同じ結果を返します。詳しい方が居ればご教示願います。
式1(再掲)
\begin{align}
f(x)=\frac{1}{\sqrt{2\pi\sigma^2}}exp\left(-\frac{(x-\mu)^2}{2\sigma^2}\right)
\end{align}
正規分布の性質
再生性
正規分布の母数(平均と分散)はどちらも再生性を持ちます。
式6
\begin{align}
X_i \sim N(\mu_i, \sigma_i^2) \longrightarrow X_1+X_2 \sim N(\mu_1+\mu_2, \sigma_1^2+\sigma_2^2)
\end{align}
線形性
正規分布は線形性を持ちます。
式7
\begin{align}
X \sim N(\mu, \sigma^2) \longrightarrow aX+b \sim N(a\mu+b,a^2\sigma^2)
\end{align}
標準偏差と出現確率
全ての確率分布は出現確率の理論値を持ちますが、特に正規分布は検定などに頻繁に用いられるため、各範囲内の出現確率を暗記することが推奨されます。
以下のグラフは標準正規分布(平均0, 分散1)の時の出現確率を表しています。
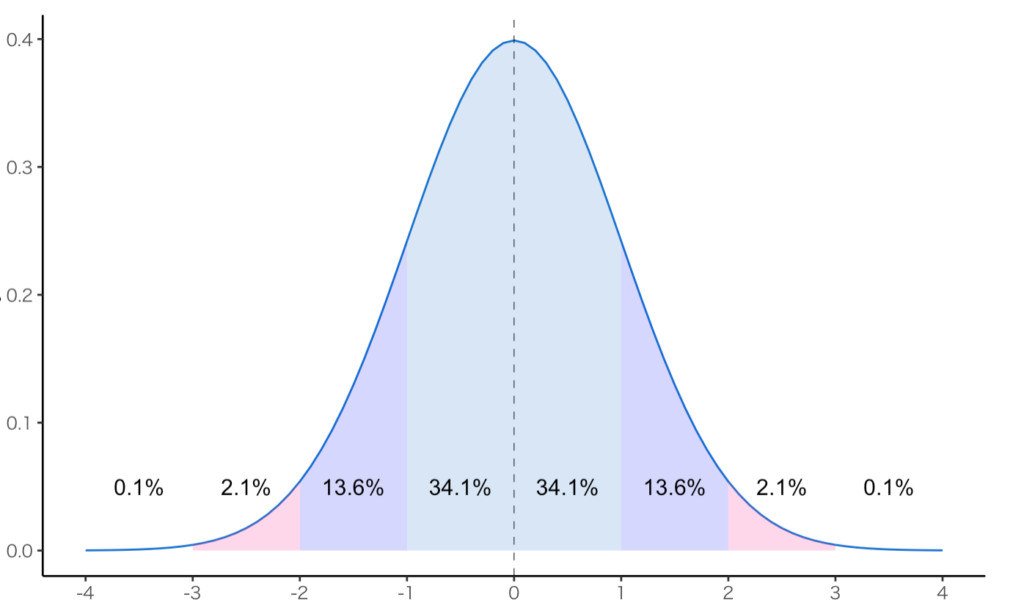
平均から±1 × 標準偏差の範囲内の値が出る確率は約68.2%になります。
この範囲を1σ(いちしぐま)と呼びます。
余談
正規分布に関連する言葉
- 千三つ: 1000回に3回程度の確率でしか起こらない出来事の例え
⇨ 3σの範囲内の値が出る確率が99.7%のため、千三つ = 3σと同義 - 6SIGMA: トヨタ社が提唱した不良品撲滅の代名詞
⇨ 6σが所以であり、不良品を数十万個に1つまで抑える施策のこと