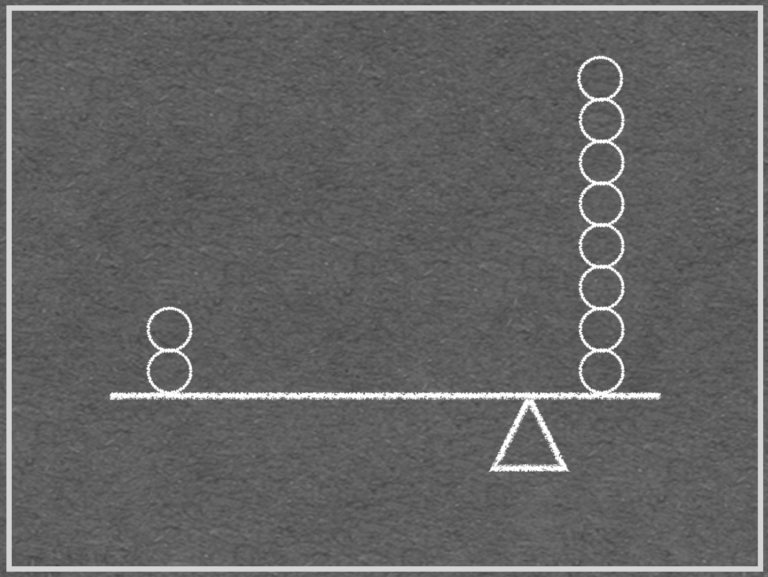
平均とは
観測した値(または取り得る値)の重心を『平均』と呼びます。
平均は数量データの代表値(統計量)の一つです。
標本の平均
標本の平均を『標本平均』と呼びます。
標本平均は『観測した値』を『観測した個数』で割って計算します。
なお、観測した値を\(x_i\)、観測した個数を\(n\)と表します。
式1
\begin{align}
\bar{x}=\frac{1}{n} \sum x_i
\end{align}
具体例
サイコロを5回振って、\(x=1,2,3,4,5\)が出た時の標本平均を計算します。
式2
\begin{align}
\bar{x}=\frac{1}{5} \sum_{i=1}^5 x_i=\frac{1+2+3+4+5}{5}=3
\end{align}
母集団の平均
母集団の平均を『母平均』と呼びます。
母平均は『取り得る値 × 値が出る確率』の総和で計算します。
なお、取り得る値を\(x_i\)、値が出る確率を\(f(x_i)\)と表します。
式3
\begin{align}
&\mu=\sum x_i \cdot f(x_i) &(1) \\
&\mu=\int x_i \cdot f(x_i) &(2) \\
\end{align}
式3-1: 離散型
式3-2: 連続型
具体例
サイコロを振った時の母平均を計算します。
なお、サイコロは全ての目が\(\frac{1}{6}\)の確率で出るものとします。
式4
\begin{align}
\mu=\sum_{i=1}^6 x_i \cdot f(x_i)=\frac{1}{6}+\frac{2}{6}+\frac{3}{6}+\frac{4}{6}+\frac{5}{6}+\frac{6}{6}=3.5
\end{align}
確率変数の平均
確率変数の平均を『期待値』と呼びます。
期待値は『取り得る値 × 値が出る確率』の総和で計算します。
なお、取り得る値を\(x_i\)、値が出る確率を\(f(x_i)\)と表します。
確率変数Xの期待値
式5
\begin{align}
&E[X]=\sum x_i \cdot f(x_i) &(1) \\
&E[X]=\int x_i \cdot f(x_i) &(2) \\
\end{align}
式5-1: 離散型の確率分布に従う確率変数\(X\)の期待値
式5-2: 連続型の確率分布に従う確率変数\(X\)の期待値
式5(確率変数\(X\)の期待値)は式4(母平均)と一致します。
式6
\begin{align}
E[X]=\mu
\end{align}
確率変数X以外の期待値
式7
\begin{align}
E[(X+1)]&=\sum (x_i+1) \cdot f(x_i) &(1) \\
E[(X-\mu)^2]&=\sum (x_i-\mu)^2 \cdot f(x_i) &(2) \\
E[A]&=\sum A \cdot f(x_i)=A &(3) \\
\end{align}
式7-1: \((X+1)\)の期待値
式7-2: \((X-\mu)^2\)の期待値
式7-3: Aの期待値
式7-3のように確率変数を含まない値も期待値を計算できます。
確率変数を含まない値は『\(E[A] = A\)』のように元の値から変化しないです。