前提知識
分散とは
数量データの代表値(統計量)の一つです。
観測した値(または取り得る値)のばらつき具合を表す値になります。
補足
- 分散が0のとき、標本が全て同じ値を取る
- 分散が大きくなるほど、標本のばらつき具合も大きくなる
標本の分散
標本の分散を『不偏分散』と呼びます。
不偏分散は『観測した値と標本平均との差の二乗和』を標本サイズ -1 で割って計算します。
なお、標本サイズを\(n\)、を\(x_i\)、標本平均を\(\bar{x}\)と表します。
式1
\begin{align}
s^2 &= \frac{1}{n-1} \sum (x_i-\bar{x})^2
\end{align}
標本サイズ -1 で割る理由は後ほど解説します。
具体例
サイコロを5回振って、\(x=1,2,3,4,5\)が出た時の分散を計算します。
式2
\begin{align}
\bar{x} &= \frac{1+2+3+4+5}{5}=3 \\
s^2 &= \frac{(1-3)^2+(2-3)^2+(3-3)^2+(4-3)^2+(5-3)^2)}{5-1}=\frac{10}{4}
\end{align}
標本分散と不偏性
標本の分散には、不偏分散の他にも標本分散と呼ばれるものが存在します。
しかし、標本分散は不偏性を持たず、基本的には使用されないため、解説を割愛します。
| 一致性 | 不偏性 | |
|---|---|---|
| 標本分散 | ○ | × |
| 不偏分散 | ○ | ○ |
母集団の分散
母集団の分散を『母分散』と呼びます。
母分散は『取り得る値と母平均との差の二乗 × 値が出る確率』で計算できます。
なお、取り得る値を\(x_i\)、母平均を\(\mu\)、値が出る確率を\(f(x_i)\)と表します。
式3
\begin{align}
\sigma^2 &= \sum (x_i-\mu)^2 \cdot f(x_i)
\end{align}
また、値が出る確率\(f(x)\)が一律の場合、式4に変形できます。
式4
\begin{align}
\sigma^2 &= \frac{1}{n}\sum (x_i-\mu)^2
\end{align}
具体例
サイコロを振った時の母分散を計算します。
なお、サイコロは全ての目が\(\frac{1}{6}\)の確率で出るものとします。
式5
\begin{align}
\mu &= \frac{1+2+3+4+5+6}{6}=3.5 \\
\sigma^2 &=\sum_{i=1}^6 (x_i-\mu)^2 \cdot f(x_i) \\
&=\frac{(1-3.5)^2}{6}+\frac{(2-3.5)^2}{6}+\frac{(3-3.5)^2}{6}+\frac{(4-3.5)^2}{6}+\frac{(5-3.5)^2}{6}+\frac{(6-3.5)^2}{6} \\
&=\frac{35}{12}
\end{align}
確率変数Xの分散
確率変数Xがとある確率分布に従います。
この時、確率変数Xの分散\(V[X]\)は、\((X-\mu)^2\)の期待値を計算することで求めることができます。
式6
\begin{align}
V[X]=E[(X-\mu)^2]=\sum (x_i-\mu)^2 \cdot f(x_i) \\
\end{align}
また、確率変数の分散は『\(X^2\)の期待値 – \(X\)の期待値の二乗』でも計算できます。
式7
\begin{align}
&V[X]=E[X^2]-E[X]^2 \\
\end{align}
証明は後ほど行います。
証明
不偏分散
標本平均とは、標本との差の総和が最も小さくなる値になります。
ここから『標本平均と標本との差の総和 ≦ 母平均と標本との差の総和』になります。言い換えると『標本分散 ≦ 母分散』の関係が成り立ち、標本分散は不偏性を持たないことが分かります。
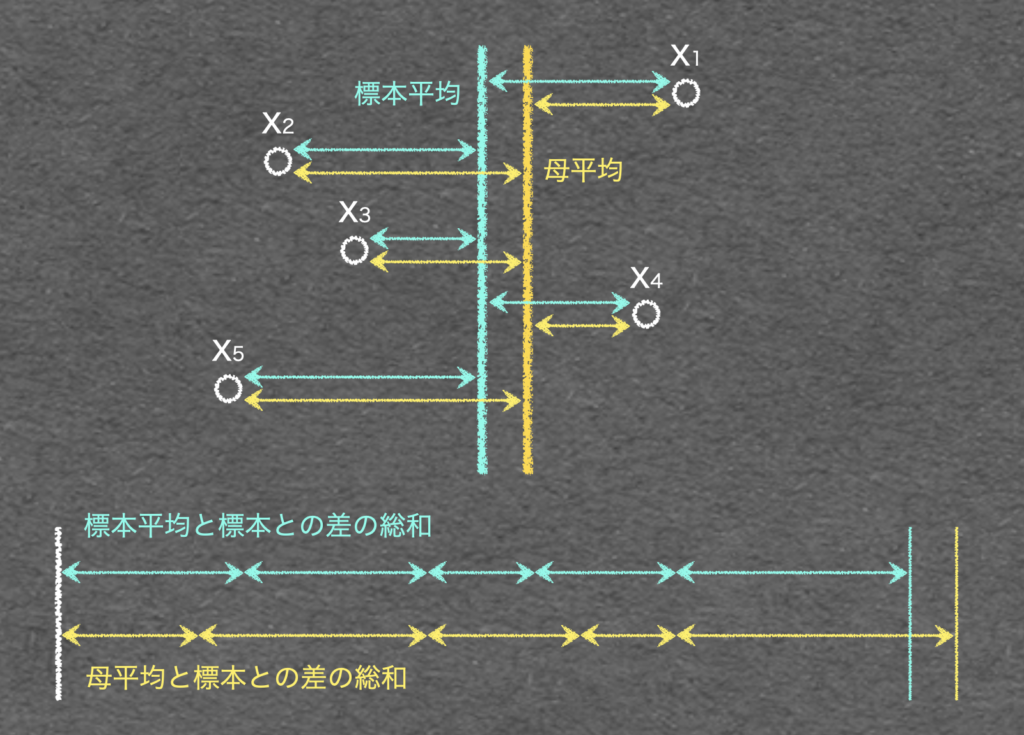
標本分散に代わり、不偏性を持つ標本の分散が不偏分散になります。
不偏分散で標本サイズ -1 を用いる理由は、以下の数式で証明できます。
式8
\begin{align}
s^2 &= \frac{1}{n} \sum (x_i-\bar{x})^2 &(1) \\
&= \frac{1}{n} \sum \left((x_i-\mu)-(\bar{x}-\mu)\right)^2 &(1.1) \\
&= \frac{1}{n} \sum \left((x_i-\mu)^2-2(x_i-\mu)(\bar{x}-\mu)+(\bar{x}-\mu)^2\right) &(1.2) \\
&= \frac{1}{n} \left(\sum (x_i-\mu)^2-\sum 2(x_i-\mu)(\bar{x}-\mu)+\sum(\bar{x}-\mu)^2\right) &(1.3) \\
&= \frac{1}{n} \left(\sum (x_i-\mu)^2-2(\bar{x}-\mu) \sum (x_i-\mu)+n(\bar{x}-\mu)^2\right) &(1.4) \\
&= \frac{1}{n} \left(\sum (x_i-\mu)^2-2n(\bar{x}-\mu)^2+n(\bar{x}-\mu)^2\right) &(1.5) \\
&= \frac{1}{n} \left(\sum (x_i-\mu)^2-n(\bar{x}-\mu)^2\right) &(1.6) \\
&= \frac{1}{n}\sum(x_i-\mu)^2-(\bar{x}-\mu)^2 &(1.7) \\
&= \sigma^2-\frac{\sigma^2}{n} &(1.8) \\
&= \frac{n-1}{n}\sigma^2 &(1.9) \\
\\
\sigma^2 &= \frac{n}{n-1} \cdot s^2 &(2) \\
&= \frac{n}{n-1} \cdot \frac{1}{n} \sum (x_i-\bar{x})^2 &(2.1) \\
&= \frac{1}{n-1} \sum (x_i-\bar{x})^2 &(2.2) \\
\end{align}
式8-1.1
母平均\(\mu\)を式に追加
式8-1.4
\(\sum (x_i-\mu)=n(\bar{x}-\mu) \longleftarrow \sum x_i=n\bar{x}\)
式8-1.7
\(\sigma^2=\frac{1}{n}\sum(x_i-\mu)^2 \longleftarrow\) 母分散
\(\frac{\sigma^2}{n}=(\bar{x}-\mu)^2 \longleftarrow\) 対数の法則
確率変数の分散
式9
\begin{align}
V[X]&=E[(X-\mu)^2] &(1) \\
&=\sum (x-\mu)^2 \cdot f(x) &(1.1) \\
&=\sum (x^2-2\mu x+\mu^2) \cdot f(x) &(1.2) \\
&=\sum x^2f(x)-2\mu \sum xf(x)+\mu^2 \sum f(x) &(1.3) \\
&=\sum x^2f(x)-2\mu \sum xf(x)+\mu^2 &(1.4) \\
&=\sum x^2f(x)-2E[X] \sum xf(x)+E[X]^2 &(1.5) \\
&=E[X^2]-2E[X]E[X]+E[X]^2 &(1.6) \\
&=E[X^2]-E[X]^2 &(1.7) \\
\end{align}
式9-1(期待値の解説を参照)
\(E[(X-\mu)^2] \rightarrow \sum (x-\mu)^2f(x)\)
式9-1.3(確率の総和は必ず1になる)
\(\sum f(x)=1\)
式9-1.4(期待値の解説を参照)
\(\mu=E[X]\)
式9-1.5(期待値の解説を参照)
\(\sum x^2f(x) \rightarrow E[X^2], \sum xf(x) \rightarrow E[X]\)