幾何分布とは
確率pで成功するベルヌーイ試行を繰り返します。
この時、成功するまでの試行回数x(または失敗回数y)を表した離散型の確率分布になります。
注意点
幾何分布には以下の2つの定義が存在します。
幾何分布がどちらの意味で利用されているか常に注意を払ってください。
- 初めて成功するまでの試行回数を表す
⇨ ここでは確率変数をXと表現します - 初めて成功するまでの失敗回数を表す
⇨ ここでは確率変数をYと表現します
事象の具体例
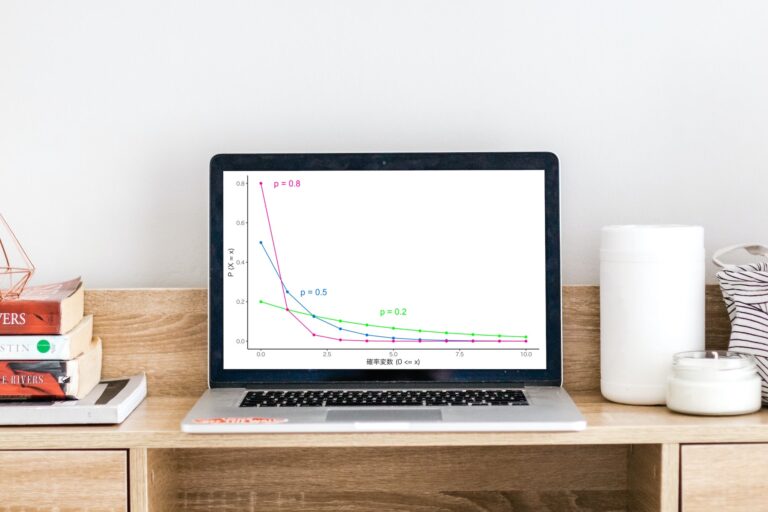
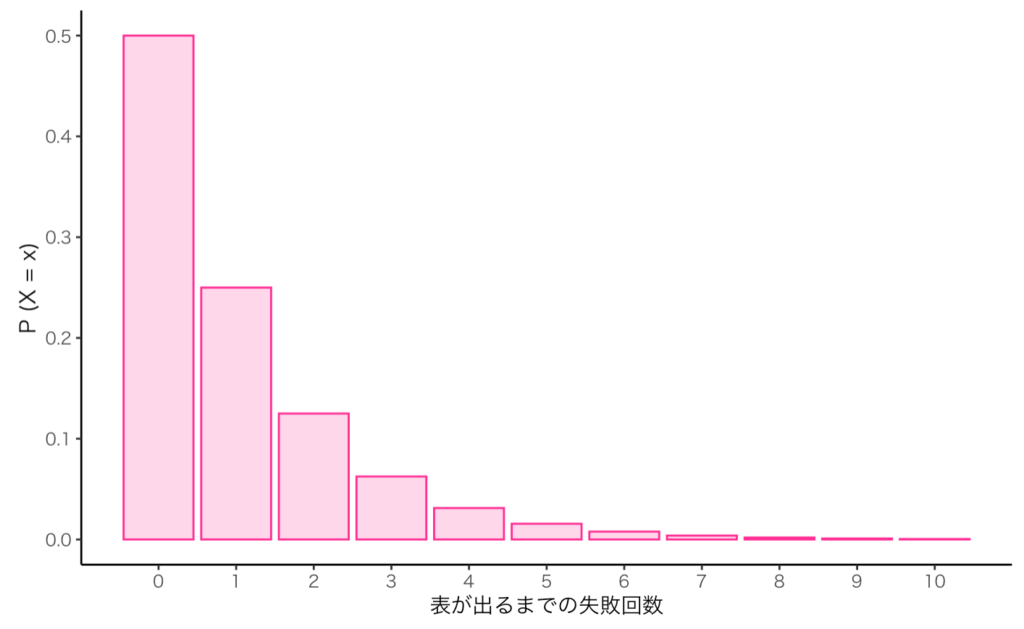
- 50%の確率で表が出るコインでコイントスを行う(グラフあり)
⇨ 表が出るまでの試行(または失敗)回数 - 排出率1%のSSRキャラが出るガチャを回す
⇨ SSRキャラが出るまでの試行(または失敗)回数 - 2%の確率でクリックされる広告を表示する
⇨ 広告がクリックされるまでに表示された試行(または失敗)回数
確率分布
\begin{align}
X \sim Ge(p) \\
Y \sim Ge(p)
\end{align}
幾何分布の確率変数と母数は以下の意味を持ちます。
なお、ここでは幾何分布を\(Ge(p)\)と表します。
- X: ベルヌーイ試行が成功するまでの試行回数
- Y: ベルヌーイ試行が成功するまでの失敗回数
- p: それぞれのベルヌーイ試行が成功する確率
確率質量関数
\begin{align}
P(X=x) &= p(1-p)^{(x-1)} \\
P(Y=y) &= p(1-p)^y
\end{align}
幾何分布の確率質量関数は以下の要素から構成されています。
- 成功する確率 \(\longrightarrow p\)
- 失敗する確率と失敗した回数 \(\longrightarrow (1-p)^{x-1}\) または \((1-p)^y\)
パターンの数
幾何分布は、成功するまでの試行(または失敗)回数を表しています。
最初の試行から失敗を繰り返し、成功するのは最後の1回だけになります。
その為、二項分布とは異なり、パターンの数は1通りに限定されます。
失敗回数と試行回数の関係
幾何分布は、数多の失敗と1回の成功から成り立ちます。
その為、失敗回数と試行回数は以下の関係を持ちます。
- 失敗回数 = 試行回数 – 1
\(\rightarrow y=(x-1)\)
性質
期待値
\begin{align}
E[X] &= \frac{1}{p} \\
E[Y] &= \frac{1-p}{p}
\end{align}
分散
\begin{align}
V[X]=V[Y] = \frac{1-p}{p^2} \\
\end{align}
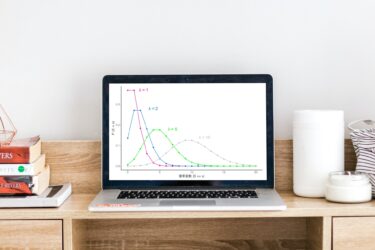
無記憶性を持つ
過去の試行が未来の試行に一切の影響を与えない性質を持ちます。
100連続で失敗した場合でも、101回目の試行の成功確率は変化しません。
関係する分布
ベルヌーイ分布
成功するまでの各試行がベルヌーイ分布に従います。
負の二項分布(パスカル分布)
幾何分布を一般化した分布になります。