ポアソン分布

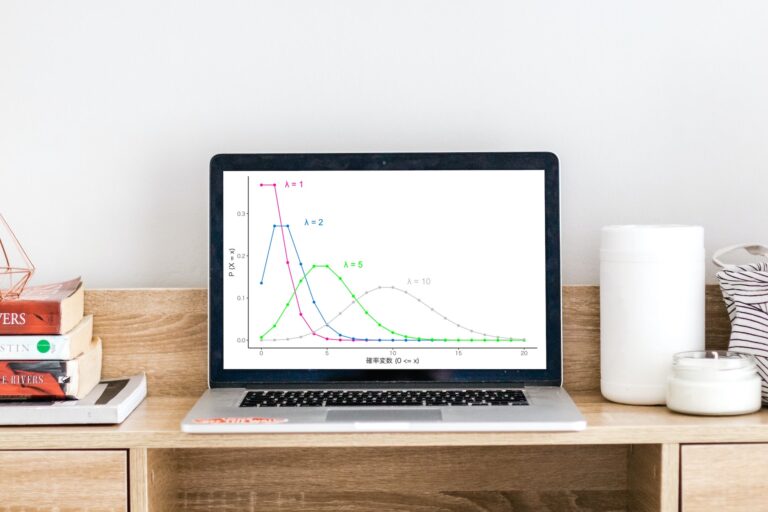
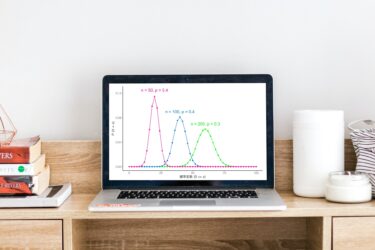
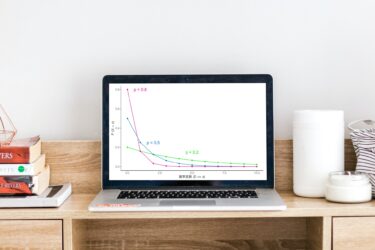
ポアソン分布とは

ある期間に平均λ回発生する事象があります。
この時、発生した事象の回数xを表した離散型の確率分布を表します。

具体的な事象の回数

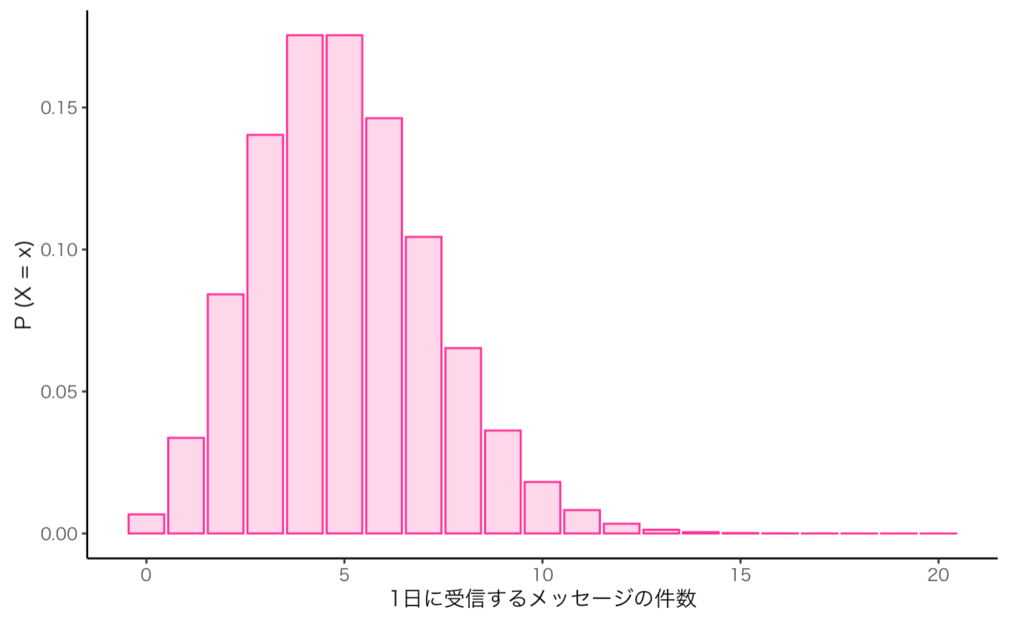
• 1日に平均5件のメッセージを受信するLINE（グラフあり）
  ⇨ 1日に受信するメッセージの件数
• 1時間に平均100台の車両が通過する交差点
  ⇨ 1時間に通過する車両の台数
• ひと月の間に平均10000回表示される広告
  ⇨ ひと月に広告を表示する回数

確率分布

ポアソン分布の確率変数と母数は以下の意味を持ちます。
なお、ここではポアソン分布を\(Po(\lambda)\)と表します。

• X: ある期間に事象が発生する回数
• \(\lambda\): ある期間に事象が発生する回数の平均値

確率質量関数

ポアソン分布の確率質量関数は二項分布から導出できます。
なお、導出には\(n=\infty, p=0, np=\lambda\)と仮定する必要があります。

\begin{align}
{}_nC_xp^x(1-p)^{n-x} \longrightarrow exp(-\lambda)\frac{\lambda^x}{x!}
\end{align}

二項分布の代替手段

ポアソン分布は二項分布の代替手段として使われることがあります。
例えば、試行回数\(n=1000\)、発生確率\(p=0.002\)の確率質量関数を考えます。

ある期間に発生する事象の回数を求める

ポアソン分布には、二項分布では対応できない独自の役割も存在します。
それが、ある期間に発生する事象の回数を求めることです。

例えば、1日の間に交差点を通過する車両の台数を考えてみましょう。
計測は単位時間ごとに行い、車両が通過したら成功、通過しなければ失敗とみなします。

この時、単位時間ごとの計測回数nと成功確率pは以下の感じで変化します。

• 1時間ごと
  ⇨ \(n=24,p=1\)
  ⇨ 成功時の通過台数: 1000台以上
• 1分ごと
  ⇨ \(n=1440,p=0.99\)ぐらい
  ⇨ 成功時の通過台数: 平均20台前後
• 1秒ごと
  ⇨ \(n=86400,p=0.2\)ぐらい
  ⇨ 成功時の通過台数: 稀に2台以上
• 無限小時間ごと
  ⇨ \(n=\infty,p=0\)
  ⇨ 成功時の通過台数: 必ず1台

このように計測間隔を無限小にすると、\(n=\infty,p=0\)の二項分布に従います。
また、成功で1台、失敗で0台の車両が通過するため、成功数が車両の通過台数になります。

この時、\(np=\lambda\)と置いたものがポアソン分布になります。

性質

期待値と分散

\begin{align}
E[X]=V[X]=\lambda
\end{align}

再生性を持つ

\begin{align}
X_i \sim Po(\lambda_i) \longrightarrow X_1+X_2 \sim Po(\lambda_1+\lambda_2)
\end{align}

関係する分布

二項分布

ポアソンの少数の法則
\(n \rightarrow \infty, p \rightarrow 0, np \rightarrow \lambda\) と置いた時、ポアソン分布を導出できます。

\begin{align}
{}_nC_xp^x(1-p)^{n-x} \longrightarrow e^{-\lambda}\lambda^x/x!
\end{align}

正規分布

λが十分大きい時に限り、正規分布は非常に優れた近似となることが知られています。

\begin{align}
Po(\lambda) \simeq N(\lambda, \lambda)
\end{align}

証明

期待値と分散がパラメータλと一致する

ポアソン分布は、\(n=\infty, p=0, np=\lambda\)と置いた時の二項分布から導出できます。
導出の方法は二項分布の解説をご覧ください。

この条件下での二項分布の期待値と分散は以下の通り表せます。

\begin{align}
E[X] &= np = \lambda \\
V[X] &= np(1-p) = \lambda(1-0) = \lambda \\
\end{align}