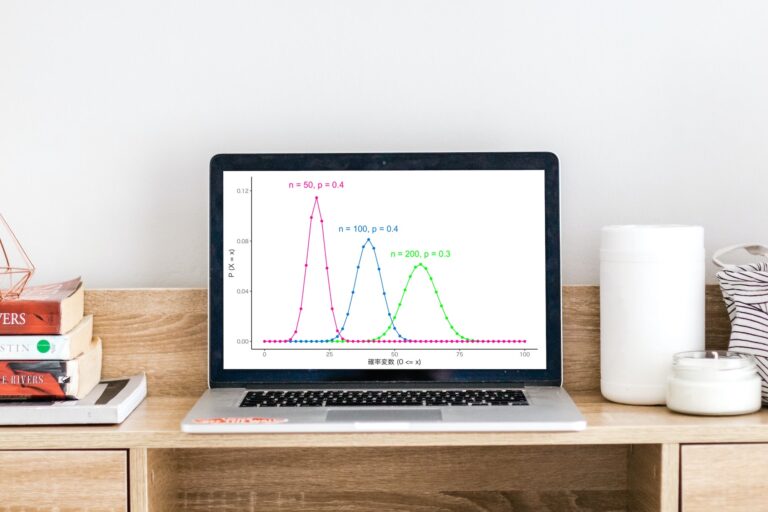
二項分布とは
確率pで成功するベルヌーイ試行をn回繰り返します。
この時、成功した事象の回数xを表した離散型の確率分布になります。
具体的な事象の回数
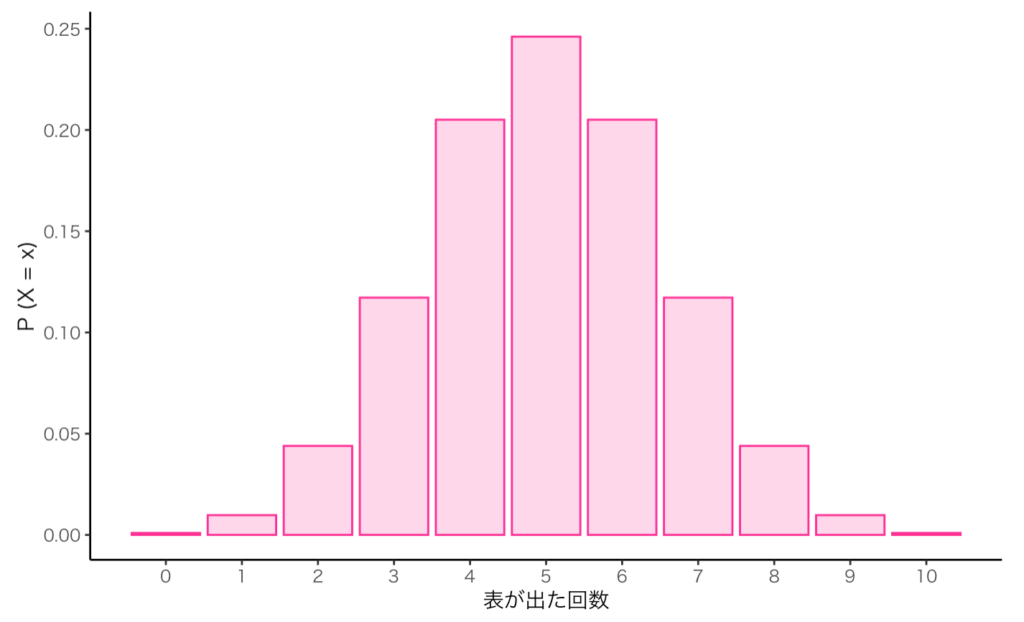
- 50%の確率で表が出るコインを10回コイントスする(グラフあり)
⇨ 表が出た回数 - 1/6の確率で1の目が出るサイコロを20個振る
⇨ 1の目が出た回数 - 1%の確率でSSRのキャラが排出されるガチャを100連回す
⇨ SSRのキャラが排出された回数 - 2%の確率でクリックされる広告を1000回表示する
⇨ クリックされた回数
確率分布
\begin{align}
X \sim B(n, p)
\end{align}
二項分布の確率変数と母数は以下の意味を持ちます。
なお、ここでは二項分布を\(B(n,p)\)と表します。
- X: ベルヌーイ試行が成功した回数
- n: ベルヌーイ試行を繰り返した回数
- p: それぞれのベルヌーイ試行が成功する確率
確率質量関数
\begin{align}
P(X=x)={}_nC_xp^x(1-p)^{n-x}
\end{align}
二項分布の確率質量関数は以下の要素から構成されます。
- 二項係数 \(\longrightarrow {}_nC_x\)
- 成功する確率と成功した回数 \(\longrightarrow p^x\)
- 失敗する確率と失敗した回数 \(\longrightarrow (1-p)^{n-x}\)
二項係数
二項係数はパターンの数を表しています。
例えば、コイントスを2回行った時のパターンは以下の通りです。
- 表が2回出るパターンは1通り(○○)
\(\rightarrow {}_2C_2=1\) - 表と裏が1回ずつ出るパターンは2通り(○● または ●○)
\(\rightarrow {}_2C_1=2\) - 裏が2回出るパターンは1通り(●●)
\(\rightarrow {}_2C_0=1\)
「成功する確率と成功した回数」と「失敗する確率と失敗した回数」
二項係数を除いた要素はパターンの数を考慮しない確率を表しています。
二項係数と同じコイントスを例として扱いましょう。
表が出ることを成功とみなし、成功する確率を\(p=0.6\)と仮定します。
- 表が2回出る確率
\(\rightarrow 0.6^2=0.36\) - 表と裏が1回ずつ出る確率
\(\rightarrow 0.6*0.4=0.24\) - 裏が2回出る確率
\(\rightarrow 0.4^2=0.16\)
この時の合計は\(0.36+0.24+0.16=0.76\)になります。
パターンの数を考慮していないため、当然、確率の総和が1に届きません
二項係数の例で求めた通り、表と裏が1回ずつ出るパターンは2通り存在します。
つまり、パターンの数を考慮することで\(0.36+0.24*2+0.16=1\)になります。
性質
期待値
期待値は、試行回数 × 成功確率で求まります。
\begin{align}
E[X]&=np \\
\end{align}
分散
分散は、成功確率\(p=[0,1]\)の時は0になり、\(p=0.5\)の時が最大になります。
\begin{align}
V[X]&=np(1-p)
\end{align}
再生性を持つ
成功確率pが一致していることが前提条件になります。
\begin{align}
X_i \sim B(n_i, p) \longrightarrow X_1+X_2 \sim B(n_1+n_2, p)
\end{align}
関係する分布
ベルヌーイ分布
試行回数\(n=1\)の時に一致します。
なお、\(Be(p)\)はベルヌーイ分布を表します。
\begin{align}
B(1, p)=Be(p)
\end{align}
ポアソン分布
\(n=\infty, p=0, np=\lambda\)の時に近似します。
二項分布がポアソン分布に近似する性質をポアソンの少数の法則とも呼びます。
正規分布
nが十分に大きく、期待値と分散も十分に大きい時に限り、正規分布は非常に優れた近似となることが知られています。
正規分布に従うと仮定した時、多くの場合、二項分布に従うと読み替えることができます。
この性質により、期待値と分散を求めることが容易となります。
証明
期待値
\begin{align}
E[X] &= \sum_{x=0}^{n} x P(X=x) \\
&= \sum_{x=0}^{n} x {}_nC_xp^x(1-p)^{n-x} \\
&= \sum_{x=0}^{n} x \frac{n!}{x!(n-x)!} p^x(1-p)^{n-x} \\
&= \sum_{x=0}^{n} x \frac{np}{x} \frac{(n-1)!}{(x-1)!(n-x)!} p^{x-1}(1-p)^{n-x} \longleftarrow n, p, x \text{を1つずつ拝借} \\
&= np \sum_{x=0}^{n} \frac{(n-1)!}{(x-1)!(n-x)!} p^{x-1}(1-p)^{n-x} \\
&= np \sum_{x=0}^{n} \frac{(n-1)!}{(x-1)!((n-1)-(x-1))!} p^{x-1}(1-p)^{(n-1)-(x-1)} \\
&= np \sum_{x=0}^{n} {}_{n-1}C_{x-1} p^{x-1}(1-p)^{(n-1)-(x-1)} \\
&= np \cdot (p + (1-p))^{n-1} \longleftarrow \text{二項定理} \\
\\
&= np \cdot (1)^{n-1}\\
\\
&= np \\
\end{align}
分散
\begin{align}
E[X^2] &= \sum_{x=0}^{n} x^2 P(X=x) \\
&= \sum_{x=0}^{n} (x+x(x-1)) P(X=x) \\
&= \sum_{x=0}^{n} x P(X=x) + \sum_{x=0}^{n} x(x-1) P(X=x) \\
&= np + \sum_{x=0}^{n} x(x-1) P(X=x) \longleftarrow np=E[X]=\sum_{x=0}^{n} x P(X=x) \\
&= np + \sum_{x=0}^{n} x(x-1) {}_nC_xp^x(1-p)^{n-x} \\
&= np + \sum_{x=0}^{n} x(x-1) \frac{n!}{x!(n-x)!}p^x(1-p)^{n-x} \\
&= np + \sum_{x=0}^{n} x(x-1) \frac{n(n-1)p^2}{x(x-1)} \frac{(n-2)!}{(x-2)!(n-x)!}p^{x-2}(1-p)^{n-x} \longleftarrow \text{拝借} \\
&= np + n(n-1)p^2 \sum_{x=0}^{n} \frac{(n-2)!}{(x-2)!(n-x)!}p^{x-2}(1-p)^{n-x} \\
&= np + (np)^2-np^2 \sum_{x=0}^{n} \frac{(n-2)!}{(x-2)!(n-x)!}p^{x-2}(1-p)^{n-x} \\
&= np + (np)^2-np^2 \sum_{x=0}^{n} \frac{(n-2)!}{(x-2)!((n-2)-(x-2))!}p^{x-2}(1-p)^{(n-2)-(x-2)} \\
&= np + (np)^2-np^2 \sum_{x=0}^{n} {}_{n-2}C_{x-2}p^{x-2}(1-p)^{(n-2)-(x-2)} \\
&= np + (np)^2-np^2 \cdot (p+(1-p))^{n-2} \longleftarrow \text{二項定理} \\
\\
&= np + (np)^2-np^2 \cdot (1)^{n-2} \\
\\
&= np+(np)^2-np^2 \\
\\
\\
V[X] &= E[X^2]-E[X]^2 \\
\\
&= np+(np)^2-np^2-(np)^2 \\
\\
&= np(1-p) \\
\end{align}
ポアソン分布の導出
\(n=\infty, p=0, np=\lambda\)と仮定します
\begin{align}
P(X=x) &= {}_nC_xp^x(1-p)^{n-x} \\
&= \frac{n!}{x!(n-x)!}p^x(1-p)^{n-x} \\
&= \frac{n!}{(n-x)!}(1-p)^{n-x}\frac{p^x}{x!} \\
&= \left(n(n-1)…(n-x+1)\right)(1-p)^{n-x}\frac{p^x}{x!} \\
&= \left(n(n-1)…(n-x+1)\right)(1-p)^{n-x}\frac{p^x}{x!} \cdot \frac{n^x}{n^x} \longleftarrow \text{ポイント} \\
&= \left(\frac{n(n-1)…(n-x+1)}{n^x}\right)(1-p)^{n-x}\frac{(np)^x}{x!} \\
&= \left(\frac{n}{n}\frac{(n-1)}{n}…\frac{(n-x+1)}{n}\right)(1-p)^{n-x}\frac{(np)^x}{x!} \longleftarrow \text{nからn-x+1までx個} \\
&= \left(\frac{n}{n}\frac{n}{n}…\frac{n}{n}\right)(1-p)^{n}\frac{(np)^x}{x!} \longleftarrow n=\infty\text{と仮定} \\
&= (1-p)^{n}\frac{(np)^x}{x!} \\
&= \left(1-\frac{\lambda}{n}\right)^{n}\frac{\lambda^x}{x!} \longleftarrow np=\lambda,p=\frac{\lambda}{n}\text{と仮定} \\
&= exp(-\lambda)\frac{\lambda^x}{x!} \longleftarrow \text{指数関数} \\
\end{align}