Point
ここからStep.2の後半(本質の解説パート)に入ります。
確率変数とは何か
確率変数とは
観測値(データ)は本質からランダムに決まると解説してきました。この時、確率変数を以下の通り定義しましょう。
定義
『データの本質』
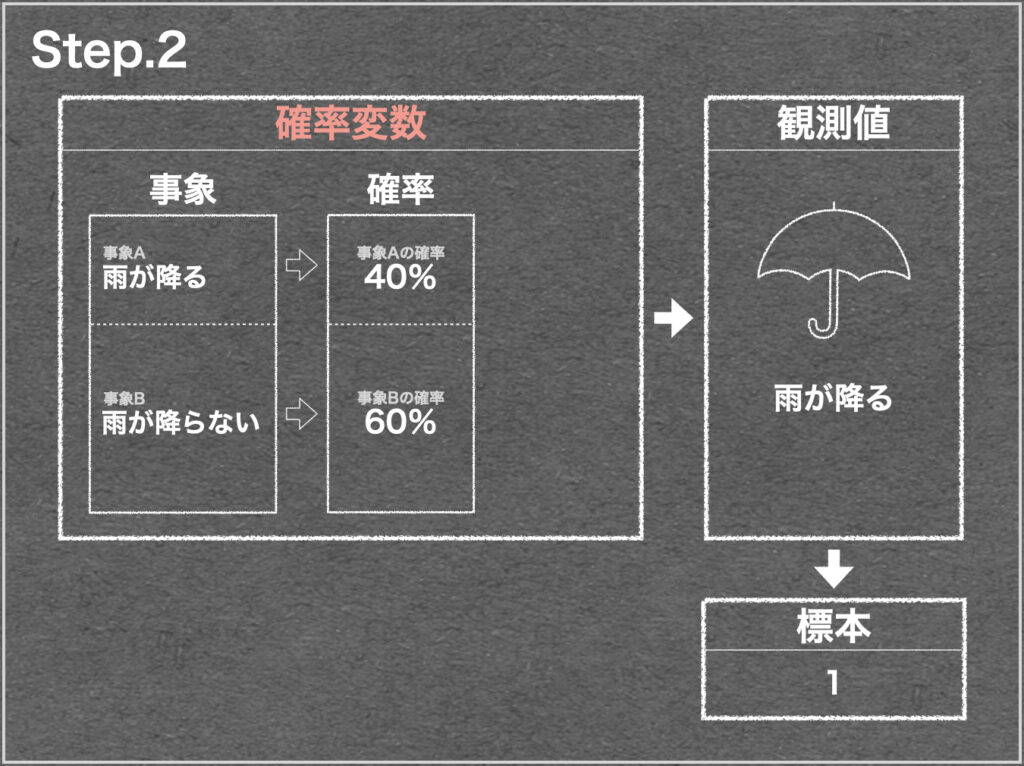
確率変数の形状
これまで『本質』と呼んできた正体を『確率変数』と定義しました。
確率変数は『事象と確率の組み合わせ』の他にも要素を持つことがあり、形状は『種類 × 特徴』の数だけ存在します。詳しくは次のページで解説します。
種類の具体例
- 事象が裏表のように二択を表す
⇨ 降水確率 - 全ての事象が同じ確率で発生する
⇨ サイコロ - 平均値に近い値が起こりやすい
⇨ IQや偏差値
特徴の具体例
- 確率が変化する
⇨ 降水確率40%と90% - 事象の数が変化する
⇨ 6面ダイスと100面ダイス - 平均値やばらつきが変化する
⇨ IQの平均値は100, 偏差値の平均値は50
表記
特別な理由がない限り、確率変数は\(X,Y,Z\)などの大文字を使って表現します。
式1
\begin{align}
X=\left\{
\begin{array}{ll}
&\text{雨が降る} &\rightarrow 40\% \\
&\text{雨が降らない} &\rightarrow 60\% \\
\end{array}
\right.
\end{align}
確率の表現
確率変数が値を取る確率を式2の通り表現します。
式2
\begin{align}
&P(X=x)=f(x) &(1) \\
&P(X=1)=0.4 &(2)
\end{align}
式2-1
確率変数がxを取る確率は\(f(x)\)
式2-2
確率変数が『雨が降る = 1』を取る確率は40%