諸注意
- 問題本文は公式サイトまたは公式問題集を参照してください
- 統計検定2級に合格している方を想定して解説していきます
問題8-1
217点の観測データ \(y_i(i=1,2,…,217)\) に対して式1(FusedLasso)を用いて平滑化を行う。\(\lambda=500\)の時、平滑化した結果のグラフを答えよ。
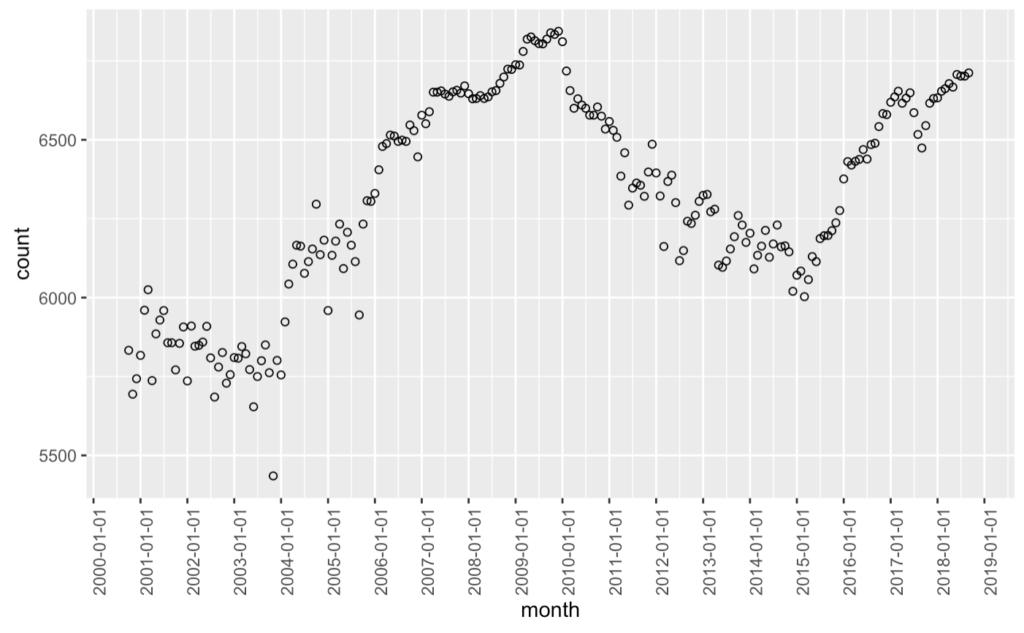
式1
\begin{align}
\newcommand{\argmin}{\mathop{\rm arg~min}\limits}
\hat{\beta}=\argmin_{\beta \in R^{217}} \frac{1}{2} \sum^{217}_{i=1}(y_i-\beta_i)^2+\lambda \sum^{216}_{i=1} |\beta_{i+1}-\beta_i| \\
\end{align}
選択肢
公式問題集を参照してください
答え 選択肢 ④
解説
前提知識
Lasso回帰とはL1ノルム(絶対値の和)を採用した平滑化手法であり、特徴としてスパース性を持ちます。スパース性とは変化が乏しい箇所の係数が0になるという性質であり、Lasso回帰を用いた平滑化後のグラフは階段状に変化します。
選択肢
選択肢の中からグラフが階段状に変化しているのは選択肢4になります。
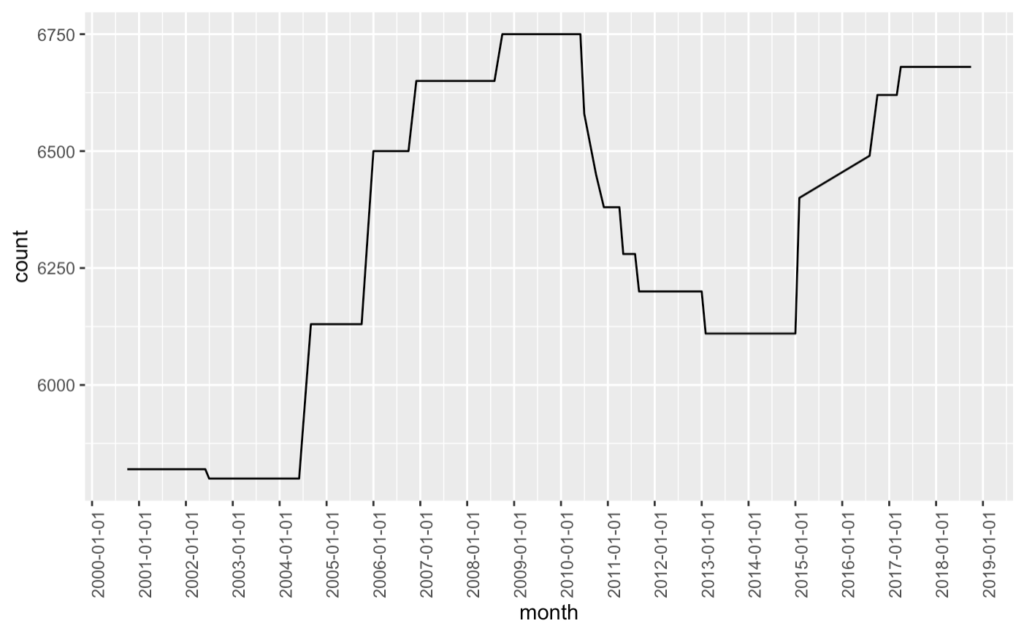
したがって、選択肢4が正解になります。
別解
損失関数と正則関数
Lasso回帰の特性を知らない場合は、式1(Fused Lasso)の意味を考える必要があります。この関数は、損失関数と正則関数に分解することができます。それぞれの関数で最適化を行うと、\(\beta_i\)の値は以下の通りとなります。
- 損失関数: \(\frac{1}{2}\sum^{217}_{i=1}(y_i-\beta_i)^2\)
⇨ 観測値と平滑化後のデータの差が0になる - 正則関数: \(\lambda\sum^{216}_{i=1} |\beta_{i+1}-\beta_i|\)
⇨ 平滑化後のデータの前後の差が0になる(切片は何でもよい)
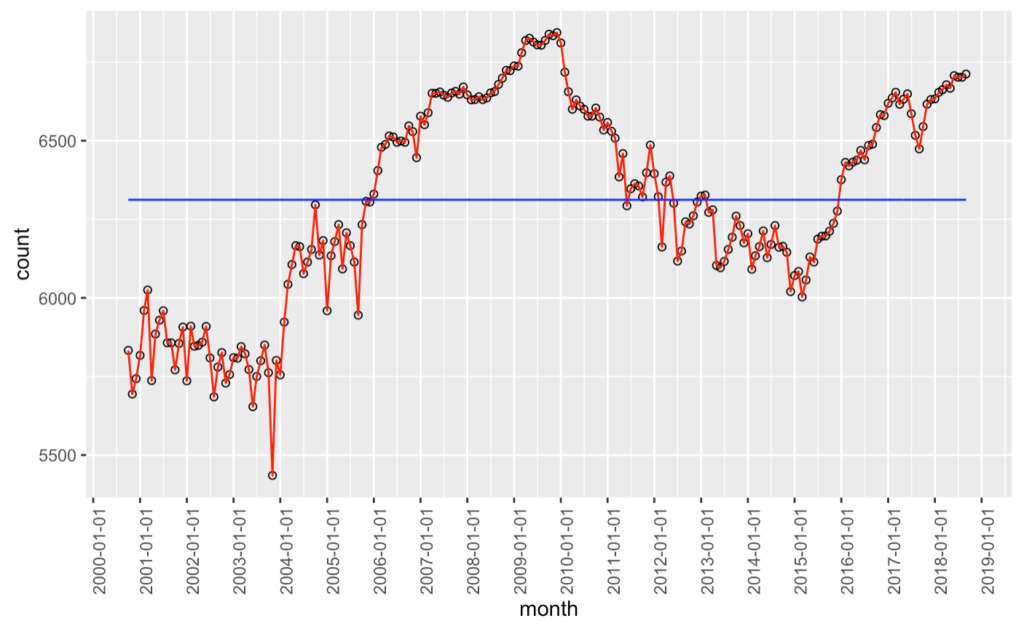
ここから損失関数と正則関数の和が最も小さくなる組み合わせは、前後の観測値の差が小さい区間では水平に区間の平均値を移動し、前後の観測値の差が大きい箇所でのみ上下に大きく変化するグラフになります。
したがって、正則関数の特徴(変化が小さい区間では区間の平均値を水平に移動する性質)を持つ選択肢4が正解になります。
問題8-2
問題8-1と同じデータに対して別の平滑化手法を適用した。この結果に対応する平滑化手法として適切なものを答えよ。
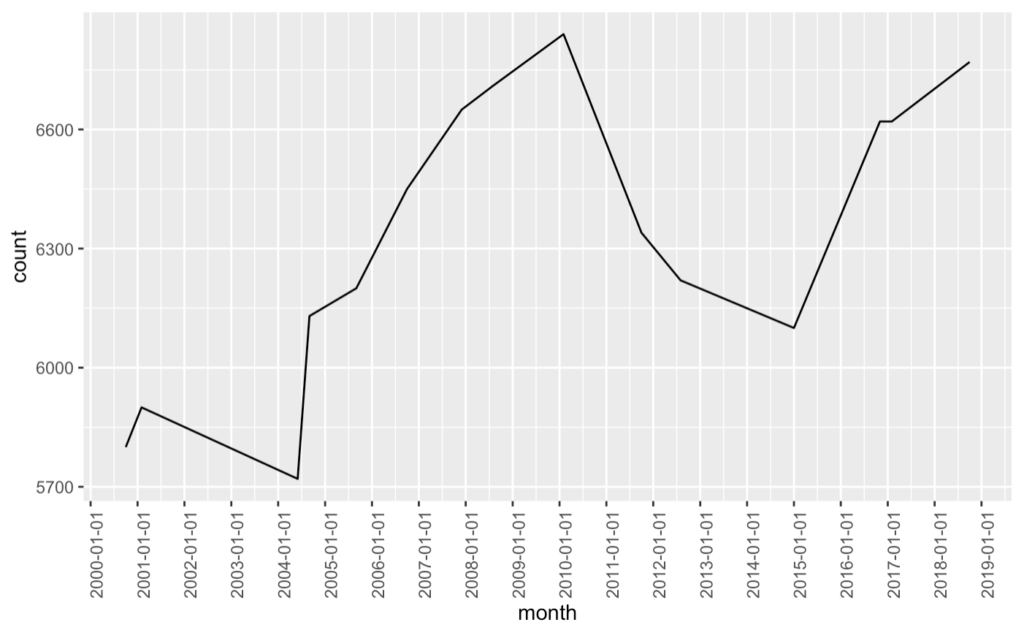
選択肢
\begin{align}
\newcommand{\argmin}{\mathop{\rm arg~min}\limits}
1. \quad \hat{\beta} &= \argmin_{\beta \in R^{217}} \frac{1}{2} \sum^{217}_{i=1}|y_i-\beta_i|+100 \sum^{217}_{i=1} \beta_{i}^2 \\
2. \quad \hat{\beta} &= \argmin_{\beta \in R^{217}} \frac{1}{2} \sum^{217}_{i=1}|y_i-\beta_i|+500 \sum^{217}_{i=1} |\beta_{i}| \\
3. \quad \hat{\beta} &= \argmin_{\beta \in R^{217}} \frac{1}{2} \sum^{217}_{i=1}(y_i-\beta_i)^2+500 \sum^{217}_{i=1} |\beta_{i}| \\
4. \quad \hat{\beta} &= \argmin_{\beta \in R^{217}} \frac{1}{2} \sum^{217}_{i=1}(y_i-\beta_i)^2+500 \sum^{215}_{i=1} |\beta_{i+2}-2\beta_{i+1}+\beta_i| \\
5. \quad \hat{\beta} &= \argmin_{\beta \in R^{217}} \frac{1}{2} \sum^{217}_{i=1}(y_i-\beta_i)^2+500 \sum^{214}_{i=1} |\beta_{i+3}-3\beta_{i+2}+3\beta_{i+1}-\beta_i| \\
\end{align}
答え ④ \(\hat{\beta}=\argmin_{\beta \in R^{217}} \frac{1}{2} \sum^{217}_{i=1}(y_i-\beta_i)^2+500 \sum^{215}_{i=1} |\beta_{i+2}-2\beta_{i+1}+\beta_i|\)
解説
選択肢①の正則化項は\(\sum^{217}_{i=1} \beta_{i}^2\)になります。
平滑化後のデータ\(\beta_i\)が最小になる組み合わせは\(\beta_i=0\)になるため、\(\beta_i\)が\(y_i\)よりも0に近い値を取りやすくなります。しかし、本問で示された平滑化後のグラフの値\(\beta_i\)は、\(y_i\)と比較して0に近い傾向は見られません。よって、選択肢①は不正解になります。
選択肢②③の正則化項は\(\sum^{217}_{i=1} |\beta_i|\)になります。
こちらも\(\beta_i\)が最小になる組み合わせは\(\beta_i=0\)になるため、選択肢②③は不正解になります。
選択肢④の正則化項は\(\sum^{215}_{i=1} |\beta_{i+2}-2\beta_{i+1}+\beta_i|\)になります。
変換すると\(\sum^{215}_{i=1} |(\beta_{i+2}-\beta_{i+1})-(\beta_{i+1}-\beta_i)|\)になるため、\(\beta_i\)が最小になる組み合わせは\((\beta_{i+2}-\beta_{i+1})=(\beta_{i+1}-\beta_i)\)になります。言い換えると、傾きが常に同じグラフになります。本問で示された平滑化後のグラフは傾きが一定の区間が多いため、選択肢④が正解になります。
選択肢⑤の正則化項は\(\sum^{214}_{i=1} |\beta_{i+3}-3\beta_{i+2}+3\beta_{i+1}-\beta_i|\)になります。
変換すると、\(\sum^{214}_{i=1} (|\beta_{i+3}-2\beta_{i+2}+\beta_{i+1}|)-(|\beta_{i+2}-2\beta_{i+1}+\beta_i|)\)になります。これは傾きの差の差を表しており、指数関数的に成長するグラフで\(\beta_i\)が最小になります。しかし、本問で示された平滑化後のグラフは直線の区間が多く、指数関数的(曲線)なグラフではありません。よって、選択肢⑤は不正解になります。



