諸注意
- 問題本文は公式サイトまたは公式問題集を参照してください
- 統計検定2級に合格している方を想定して解説していきます
問題7-1
平均\(\mu\)が未知, 分散\(\sigma^2\)が既知の正規分布に従うサイズ1の標本Xが観測された。この時、\(\mu\)に対する事前分布として正規分布\(N(\mu_0, \sigma^2_0)\)を仮定した時、事後分布が従う正規分布\(N(\tilde{\mu}, \tilde{\sigma}^2)\)の平均と分散を答えよ。
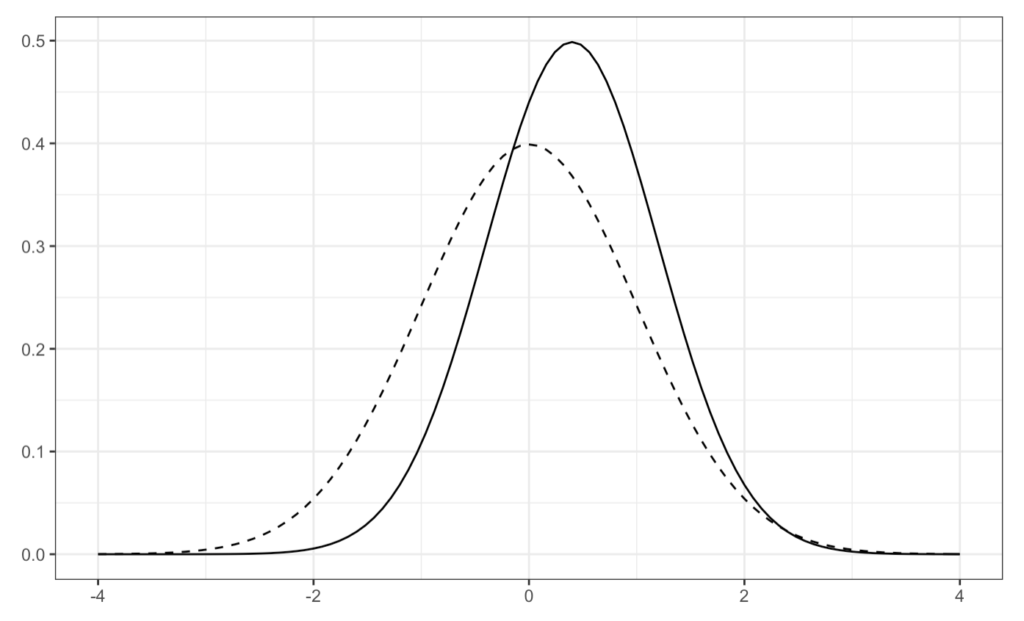
なお、\(\mu_0=0, \sigma^2_0=1, \sigma^2=4\)の時に観測値\(X=2\)が得られた場合の事前分布(波線)と事後分布(実線)の密度関数のグラフはそれぞれ以下の通りである。
選択肢
\begin{align}
1. \quad\tilde{\mu} &= \frac{\sigma^2X+\sigma_0^2\mu_0}{\sigma^2+\sigma_0^2}, \quad\tilde{\sigma}^2 = \sigma\sigma_0 \\
2. \quad\tilde{\mu} &= \frac{\sigma^2X+\sigma_0^2\mu_0}{\sigma^2+\sigma_0^2}, \quad\tilde{\sigma}^2 = \frac{\sigma^2+\sigma_0^2}{2} \\
3. \quad\tilde{\mu} &= \frac{\sigma^2X+\sigma_0^2\mu_0}{\sigma^2+\sigma_0^2}, \quad\tilde{\sigma}^2 = \left(\frac{1}{\sigma^2}+\frac{1}{\sigma_0^2}\right)^{-1} \\
4. \quad\tilde{\mu} &= \frac{\sigma_0^2X+\sigma^2\mu_0}{\sigma^2+\sigma_0^2}, \quad\tilde{\sigma}^2 = \frac{\sigma^2+\sigma_0^2}{2} \\
5. \quad\tilde{\mu} &= \frac{\sigma_0^2X+\sigma^2\mu_0}{\sigma^2+\sigma_0^2}, \quad\tilde{\sigma}^2 = \left(\frac{1}{\sigma^2}+\frac{1}{\sigma_0^2}\right)^{-1} \\
\end{align}
答え ⑤ \(\quad\tilde{\mu} = \frac{\sigma_0^2X+\sigma^2\mu_0}{\sigma^2+\sigma_0^2}, \quad\tilde{\sigma}^2 = \left(\frac{1}{\sigma^2}+\frac{1}{\sigma_0^2}\right)^{-1}\)
解説
前提知識
頻度統計から統計学に入門した方向けの説明
頻度統計学とベイズ統計学の大きな違いは、母数を不変と見るか、それとも可変と見るかの差にあります。
頻度統計学では真の値は不変であり、真の値を推定するためにデータを集めます。これに対してベイズ統計学ではデータを真として確率分布を更新していきます。
頻度主義者にとって『平均\(\mu\)が未知, 分散\(\sigma^2\)が既知の正規分布があり、\(\mu\)に対する事前分布として正規分布\(N(\mu_0, \sigma^2_0)\)を仮定した』という一文は馴染みがないため、最初は理解に苦しむと思います。
これは母数である\(\mu\)が可変であり、とりあえず母数\(\mu\)が正規分布\(N(\mu_0, \sigma^2_0)\)に従うと仮定しましょうと言うことを表しています。
- 式1-1:標本Xが従う確率分布
- 式1-2:標本Xが従う正規分布の母数\(\mu\)が従う確率分布
式1
\begin{align}
& X \sim N(\mu, \sigma^2) & (1) \\
& \mu \sim N(\mu_0, \sigma_0) & (2) \\
\end{align}
このように母数が更に別の確率分布に従うモデルを階層モデルと呼びます。
また、とりあえず母数が従うと仮定した確率分布のことを事前分布と呼び、観測値を用いて事前分布を更新します。この時、更新された確率分布のことを事後分布と呼び、以下の計算式で求めることができます。
式2
\begin{align}
\pi(\theta|x)= \frac{f(x|\theta)\pi(\theta)}{\int \theta f(x|\theta)\pi(\theta)d\theta} \\
\end{align}
\(\theta\)は母数, \(x\)は観測値, \(\pi(\theta|x)\)は事後分布, \(f(x|\theta)\)は尤度, \(\pi(\theta)\)は事前分布, \(\int \theta f(x|\theta)\pi(\theta)d\theta\)は周辺尤度を表す
式2を見て、パッと計算できる方はきっと少ないことでしょう。私もPCがなければ到底計算できません。そこで編み出されたのが共益事前分布と呼ばれるものになります。
共益事前分布とは『特定の確率分布である』且つ『事前分布と事後分布が同じ確率分布である』と言う2つの特徴を持つ場合に限り、計算コストを大幅に抑えて事後分布を求めることができる事前分布のことを指します。
特に観測値が分散が既知の正規分布に従う時、正規分布を共益事前分布として以下の通り事後分布の母数を計算することができます。
式3
\begin{align}
&\tilde{\mu} = \frac{\sigma_0^2X+\sigma^2\mu_0}{\sigma^2+\sigma_0^2} \\
&\tilde{\sigma}^2 = \left(\frac{1}{\sigma^2}+\frac{1}{\sigma_0^2}\right)^{-1} \\
\end{align}
共益事前分布
式3は本問の答えそのものになります。もちろん式3を知らない場合でも回答することは可能であるため、ここではその方法を解説します。
事後分布の目測
問題文より事前分布は平均(\(\mu_0\))が0, 分散(\(\sigma_0^2\))が1の標準正規分布になります。これと比較して事後分布の平均(\(\tilde{\mu}\))は0より大きく1より小さい, 分散(\(\tilde{\sigma}^2\))は1より小さいことが分かります。
問題文のグラフを再掲(波線: 事前分布, 実線: 事後分布)

選択肢の計算
選択肢として与えられた事後分布の平均\(\tilde{\mu}\)と分散\(\tilde{\sigma}^2\)の計算式に(\(\mu_0=0, \sigma^2_0=1, \sigma^2=4\))を代入して結果を求めます。
式4
\begin{align}
\quad\tilde{\mu}_{1\cdot2\cdot3} &= \frac{\sigma^2X+\sigma_0^2\mu_0}{\sigma^2+\sigma_0^2} = \frac{4 \cdot 2+1 \cdot 0}{4+1} = 1.6 \\
\\
\quad\tilde{\mu}_{4\cdot5} &= \frac{\sigma_0^2X+\sigma^2\mu_0}{\sigma^2+\sigma_0^2} = \frac{1 \cdot 2+4 \cdot 0}{4+1} = 0.4 \\
\end{align}
式5
\begin{align}
\quad\tilde{\sigma}^2_{1} &= \sigma\sigma_0 = 2 \cdot 1 = 2 \\
\\
\quad\tilde{\sigma}^2_{2\cdot4} &= \frac{\sigma^2+\sigma_0^2}{2} = \frac{4+1}{2} = 2.5 \\
\\
\quad\tilde{\sigma}^2_{3\cdot5} &= \left(\frac{1}{\sigma^2}+\frac{1}{\sigma_0^2}\right)^{-1} = \left(\frac{1}{4}+\frac{1}{1}\right)^{-1} = 0.8 \\
\end{align}
ここから目測と一致する選択肢は、平均が\(\tilde{\mu}=0.4\) (0より大きく1より小さい), 分散が\(\tilde{\sigma}^2=0.8\) (1より小さい)になります。
したがって、選択肢⑤が正解になります。
問題7-2
サイズ10の標本Xが観測され、平均が16.71, 標準偏差が3.07であった。この時、平均に対する事前分布として正規分布\(N(13, 2.7^2)\)を仮定した時、事前分布と事後分布の密度関数のグラフとして最も適切なものを選べ。
選択肢
公式問題集を参照してください
答え グラフ ②
解説
事後分布の計算式
問題7-1より平均に対する事後分布の平均と分散は以下の式で求めることができます。また、事前分布を正規分布と仮定しているため、事後分布が正規分布ではない選択肢③と④は答えから除外します。
式3(再掲)
\begin{align}
&\tilde{\mu} = \frac{\sigma_0^2X+\sigma^2\mu_0}{\sigma^2+\sigma_0^2} \\
&\tilde{\sigma}^2 = \left(\frac{1}{\sigma^2}+\frac{1}{\sigma_0^2}\right)^{-1} \\
\end{align}
中心極限定理
本問では、正規分布に従う標本数が10件のため、標本Xの平均は以下の式に従います。
式6
\begin{align}
& \bar{X} = N(\mu, \sigma^2/10) \\
\end{align}
式6より、式3を(\(X \rightarrow \bar{X}, \sigma^2 \rightarrow \sigma^2/10\))に代替して事後分布を計算します。
式7
\begin{align}
&\tilde{\mu} = \frac{\sigma_0^2\bar{X}+(\sigma^2/10)\mu_0}{(\sigma^2/10)+\sigma_0^2} = \frac{2.7^2 \cdot 16.71+(3.07^2/10) \cdot 13}{(3.07^2/10)+2.7^2} = 16.28 \\
&\tilde{\sigma}^2 = \left(\frac{1}{(\sigma^2/10)}+\frac{1}{\sigma_0^2}\right)^{-1} = \left(\frac{1}{(3.07^2/10)}+\frac{1}{2.7^2}\right)^{-1} = 0.83 \\
\end{align}
グラフ化
- 事前分布:\(N(13, 2.7^2)\)
- 事後分布:\(N(16.28, 0.83^2)\)
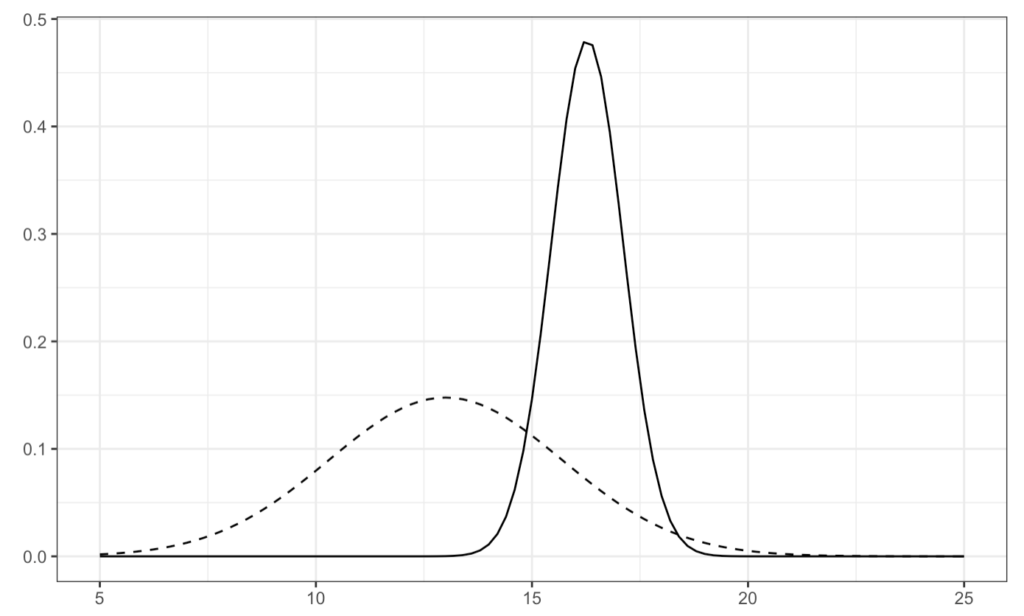
したがって、選択肢②のグラフが正解になります。
問題7-3
事後分布と同じ分布属に属する性質を持つ事前分布を共役事前分布と呼びます。この時、共役事前分布の説明として適切なものを答えよ。
選択肢
解説を参照してください
答え 選択肢①と③が正しい
解説
- 共役事前分布の利点の一つは、事後分布の計算がハイパーパラメータの更新として表現できる点である。
⇨ 正解(事前分布と事後分布が同じ確率分布に属するため、パラメータのみが更新されます)
- 正規分布の平均が既知で分散が未知のとき、分散に対する共役事前分布はベータ分布になる。
⇨ 不正解(逆ガンマ分布)
- 共役事前分布を用いることができない場合は、一般にモンテカルロ法等の数値計算を用いて事後分布を近似計算する。
⇨ 正解(事前分布と事後分布が異なる確率分布に属する場合は計算コストが重くなりやすいため、一般的にはモンテカルロ法等の近似計算を用います)
余談
『確率分布』と『母数』と『共益事前分布と事後分布』の組み合わせ
| 確率分布 | 母数 | 共益事前分布と事後分布 |
|---|---|---|
| ベルヌーイ分布 | 成功確率 | ベータ分布 |
| 二項分布 | 成功確率 | ベータ分布 |
| 正規分布 | 期待値 | 正規分布 |
| 正規分布 | 分散 | 逆ガンマ分布 |
| ポアソン分布 | 期待値 | ガンマ分布 |
| 多項分布 | 期待値 | ディリクレ分布 |



