諸注意
- 問題本文は公式サイトまたは公式問題集を参照してください
- 統計検定2級に合格している方を想定して解説していきます
問題6-1
以下の表は、説明変数 x1, …, x8 について相関係数行列を用いた主成分分析を行った結果である。この時、累積寄与率が80%以上になる主成分を答えよ。
| 主成分 | PC1 | PC2 | PC3 | PC4 | PC5 | PC6 | PC7 | PC8 | |
| 固有値 | 2.334 | 1.540 | 1.372 | 1.012 | 0.936 | 0.659 | 0.113 | 0.035 | |
| 寄与率 | 0.292 | 0.193 | 0.172 | 0.127 | 0.117 | 0.082 | 0.014 | 0.004 | |
| 固有ベクトル | x1 | 0.288 | -0.349 | 0.454 | -0.533 | 0.034 | -0.158 | 0.057 | -0.504 |
| x2 | -0.416 | 0.316 | 0.374 | 0.212 | 0.191 | 0.485 | 0.224 | -0.468 | |
| x3 | 0.250 | 0.578 | -0.353 | 0.023 | 0.095 | -0.469 | 0.277 | -0.415 | |
| x4 | -0.593 | -0.014 | -0.018 | -0.006 | -0.041 | -0.448 | -0.610 | -0.272 | |
| x5 | 0.461 | 0.474 | 0.206 | -0.049 | 0.014 | 0.266 | -0.668 | 0.016 | |
| x6 | -0.021 | -0.202 | -0.693 | -0.299 | 0.192 | 0.471 | -0.167 | -0.321 | |
| x7 | 0.301 | -0.344 | -0.058 | 0.662 | -0.401 | 0.041 | -0.105 | -0.420 | |
| x8 | -0.161 | 0.242 | -0.060 | -0.345 | -0.868 | 0.160 | 0.111 | -0.032 |
選択肢
① 第3主成分 ② 第4主成分 ③ 第5主成分 ④ 第6主成分 ⑤ 第7主成分
答え ③ 第5主成分
解説
前提知識
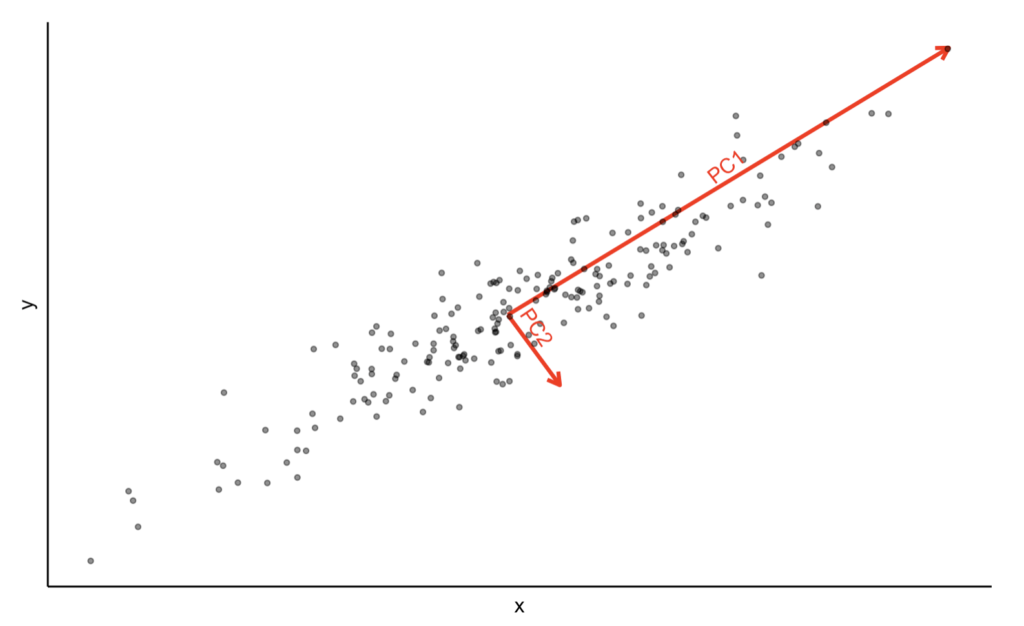
n次元のデータからばらつきが大きい(データの特徴をより捉えている)軸を取り直す作業を主成分分析と呼びます。なお、変換前の軸を説明変数、変換後の軸を主成分と呼びます。
【相関行列を用いた主成分分析の用語】
- 固有値
⇨ 説明変数のばらつきを1に固定した時の主成分のばらつきの大きさ
⇨ 固有値の合計は説明変数の量に等しい(説明変数が八個の場合は合計が8になる) - 寄与率
⇨ 固有値を説明変数の量で割った値 - 固有ベクトル
⇨ 各説明変数と主成分の相関係数
寄与率
各主成分がデータを表している度合いを寄与率と呼びます。また、第1主成分から累積した寄与率を累積寄与率と呼び、データ全体を占める表現の割合を表します。
以下は寄与率と累積寄与率を示した表になります。
| 主成分 | PC1 | PC2 | PC3 | PC4 | PC5 | PC6 | PC7 | PC8 |
| 寄与率 | 0.292 | 0.193 | 0.172 | 0.127 | 0.117 | 0.082 | 0.014 | 0.004 |
| 累積寄与率 | 0.292 | 0.485 | 0.657 | 0.784 | 0.901 | 0.983 | 0.997 | 1.001 |
ここから累積寄与率が80%以上になるのは第5主成分(選択肢③)になります。
問題6-2
横軸を第1主成分(PC1)、縦軸を第2主成分(PC2)と置いたとき、x1, x2, x3, x4 の固有ベクトルのプロットとして適切なグラフを選択肢の中から選べ。
選択肢
公式問題集を参照してください
答え グラフ ①
解説
抜粋
| 主成分 | PC1 | PC2 | |
| 固有ベクトル | x1 | 0.288 | -0.349 |
| x2 | -0.416 | 0.316 | |
| x3 | 0.250 | 0.578 | |
| x4 | -0.593 | -0.014 |
固有ベクトル
固有ベクトルとは、主成分と説明変数の相関係数を表しています。
説明変数x1はPC1と弱い正の相関があり、PC2と弱い負の相関があるため、原点から見て右下にプロットされます。同様に説明変数x2, x3, x4をプロットしたものが以下のグラフになります。
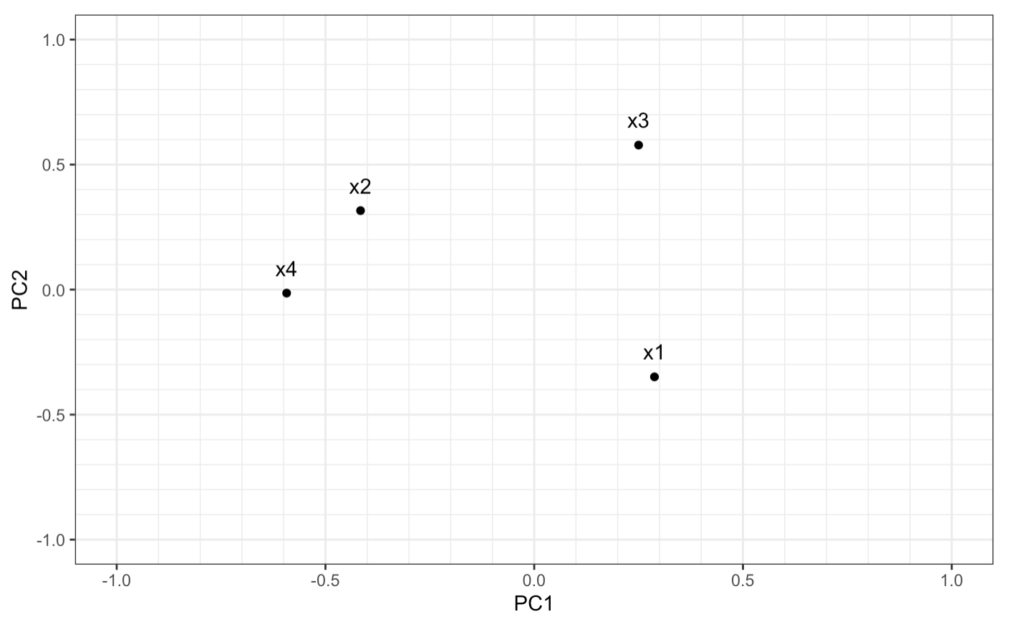
上のグラフと等しい選択肢①が正解になります。
問題6-3
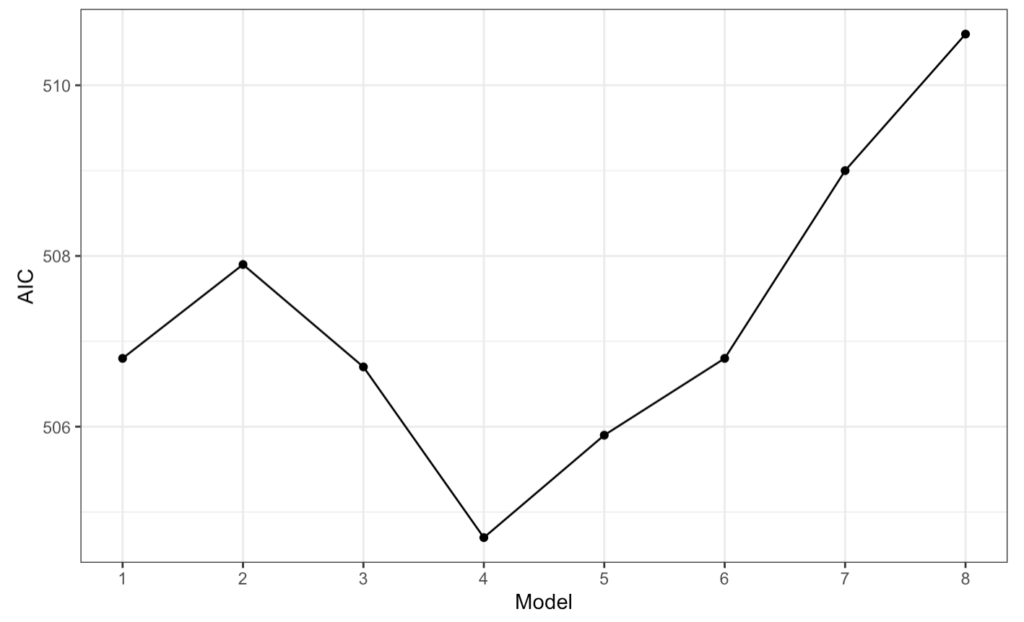
主成分スコア z1, …, z8 を説明変数にした線形回帰モデルを考える。被説明変数yを求めるため、モデル1は \(y \sim z_1\), モデル2は \(y \sim z_1+z_2\), … と階層型モデルを順にモデル8まで考える。この時の各モデルとAICが以下の関係であった時、最適なモデルを答えよ。
選択肢
① モデル2 ② モデル4 ③ モデル6 ④ モデル7 ⑤ モデル8
答え ② モデル4
解説
前提知識
AIC(赤池情報量基準)とは最適なモデルを選択するために考案された手法です。ここで言う最適なモデルとは、最大尤度L(データの適合度合い)が高く、パラメータの次数kが少ないモデルを指します。
式1(AIC)
\begin{align}
AIC = -2logL + 2(k+1)
\end{align}
最大尤度と次数の関係は準1級のレベルを超えており、私も正確に把握できていないため解説を省きますが、式1の値が小さいほど良いモデルとみなすことができます。
AIC
問題文のグラフより、AICの値が最も小さいのはモデル4になります。したがって、最適なモデルは4(選択肢2)になります。
式2(モデル4)
\begin{align}
y \sim z_1+z_2+z_3+z_4
\end{align}
余談
各モデルのAICを見ると、モデル2のAICが高いことが分かります。これは主成分\(z_2\)が説明変数として不適切である可能性を示唆しているため、実務であれば以下のモデルのAICも確認した方が良いでしょう。
式3
\begin{align}
y \sim z_1+z_3+z_4
\end{align}
問題6-4
主成分分析とAICに関する説明として正しいものを答えよ。
選択肢
解説参照
答え 選択肢 ②
解説
- 主成分分析を行う際には、前処理としてデータを標準化することが不可欠である。
⇨ データを標準化することが一般的であり、変数間の尺度が異なる場合は推奨されますが、尺度の違いが意味のある情報を含む時など、標準化を行わずに共分散行列を用いることが適切な場合もあります。
- 相関行列に対する主成分分析では、各主成分の主成分負荷量(因子負荷量)はその主成分と元の変数との相関係数と一致する。
⇨ 正解(主成分負荷量は、元の変数と主成分の関係を示すもので、主成分と元の変数との相関係数に相当します)
- AICを用いて比較できるのはモデルのパラメータ集合間に包含関係がある場合のみである。
⇨ AICはモデルの単純さと適合度を数値化して、モデル同士を比較するため、モデルのパラメータ集合間に含有関係がない場合でも比較できます。
- AICの特徴として、一般にモデル同定の一致性を持つことがあげられる。
⇨ BICの特徴になります。モデル同定の一致性とは、サンプルサイズが無限大に増えると同じモデルを選択する確率が1に収束する性質のことを指します。AICの値は、サンプルサイズが増えるに従い、適合度の値が増加しますが、単純さの評価は常に一定です。そのため、サンプルサイズが増えるに従い、複雑なモデルを評価するようになります。これに対して、BICは単純さの値もサンプルサイズに応じて変化するため、常に同じ基準でモデルを評価することができます。
- AICによるモデル選択は、交差検証法に比べて一般に計算量が大きくなるという欠点がある。
⇨ 交差検証法は学習データを何度も取り替えて、正答率の平均を求める検証手法です。中でもLOOCVは、サンプルサイズの数だけ検証を繰り返すため、非常に計算コストが重い検証手法になります。



