諸注意
- 問題本文は公式サイトまたは公式問題集を参照してください
- 統計検定2級に合格している方を想定して解説していきます
問題4-1
ある商品について、CMの影響の有無と購入の有無について調査した結果、以下の分割表が得られた。CMの影響の有無と購入の有無に関連がないと仮定した時、CMの影響あり × 購入ありの頻度の期待値を答えよ。
| 購入あり | 購入なし | 合計 | |
| CMの影響あり | 93 | 42 | 135 |
| CMの影響なし | 97 | 68 | 165 |
| 合計 | 190 | 110 | 300 |
選択肢
① 34.3 ② 48.7 ③ 58.3 ④ 85.5 ⑤ 106.7
答え ④ 85.5
解説
期待値の計算
分割表から独立であると仮定した時の期待値を計算する場合、まずは各行列の合計の割合を計算する必要があります。その後、行の合計の割合 × 列の合計の割合を計算します。
| 購入あり | 購入なし | 合計 | |
| CMの影響あり | (135 / 300) * (190 / 300) = 0.285 | (135 / 300) * (110 / 300) = 0.165 | 135 / 300 |
| CMの影響なし | (165 / 300) * (190 / 300) = 0.348 | (165 / 300) * (110 / 300) = 0.202 | 165 / 300 |
| 合計 | 190 / 300 | 110 / 300 | 300 |
この時、セルの割合の合計は必ず1 (\(=0.285+0.165+0.348+0.202\))になります。次に、算出した割合に頻度の合計を掛けることで期待値を求めることができます。
| 購入あり | 購入なし | 合計 | |
| CMの影響あり | 0.285 * 300 = 85.5 | 0.165 * 300 = 49.5 | |
| CMの影響なし | 0.348 * 300 = 104.5 | 0.202 * 300 = 60.5 | |
| 合計 | 300 |
したがって、CMの影響あり × 購入ありの頻度の期待値は85.5(選択肢④)になります。
問題4-2
CMの影響の有無と購入の有無の関連性に関するピアソンのカイ二乗統計量を求めよ。
選択肢
① -4.32 ② 0.33 ③ 3.26 ④ 10.49 ⑤ 22.93
答え ③ 3.26
解説
前提知識
- 式1:カイ二乗統計量
⇨ 偶然との乖離度合いを示す(\(x_{ij}\)は観測値, \(E[X_{ij}]\)は期待値を表す)
式1
\begin{align}
\chi^2 &= \sum_{i}\sum_{j} \frac{(x_{ij}-E[X_{ij}])^2}{E[X_{ij}]}
\end{align}
カイ二乗統計量の計算
問題4-1の結果から頻度の観測値と期待値を再掲します。なお、( )の値が期待値を表します。
| 購入あり | 購入なし | 合計 | |
| CMの影響あり | 93 (85.5) | 42 (49.5) | 135 |
| CMの影響なし | 97 (104.5) | 68 (60.5) | 165 |
| 合計 | 190 | 110 | 300 |
式1と分割表の値よりカイ二乗統計量を求めます。
式2
\begin{align}
\chi^2 = \frac{(93-85.5)^2}{85.5} + \frac{(42-49.5)^2}{49.5} + \frac{(97-104.5)^2}{104.5} + \frac{(68-60.5)^2}{60.5}= 3.26 \\
\end{align}
したがって、カイ二乗統計量は3.26(選択肢③)になります。
問題4-3
『CMの影響の有無と購入の有無には関連性がない』という帰無仮説に対する片側検定を行った。この時、帰無仮説の棄却について最も適切な選択肢を選べ。
選択肢
① 有意水準10%で棄却されない
② 有意水準10%で棄却されるが、有意水準5%で棄却されない
③ 有意水準5%で棄却されるが、有意水準2.5%で棄却されない
④ 有意水準2.5%で棄却されるが、有意水準1%で棄却されない
⑤ 有意水準1%で棄却される
答え ② 有意水準10%で棄却されるが、有意水準5%で棄却されない
解説
前提知識
カイ二乗統計量は分割表の行列が長くなるほど値が大きくなる特徴を持つため、行列の長さに応じてカイ二乗統計量の値を使い分ける必要があります。
この時、行列の長さを自由度\(\nu\)と呼び、(行数 – 1) × (列数 – 1) で求めます。
カイ二乗統計量の上側確率
問題4-2より、カイ二乗統計量が3.26であることが分かっています。また、本問の分割表は2行2列であるため、自由度は1になります。
付表3(カイ二乗分布のパーセント点)を参照した結果、自由度1のカイ二乗統計量(3.26)は上側確率10%(2.71)よりも大きく、5%(3.84)よりも小さいことが分かります。
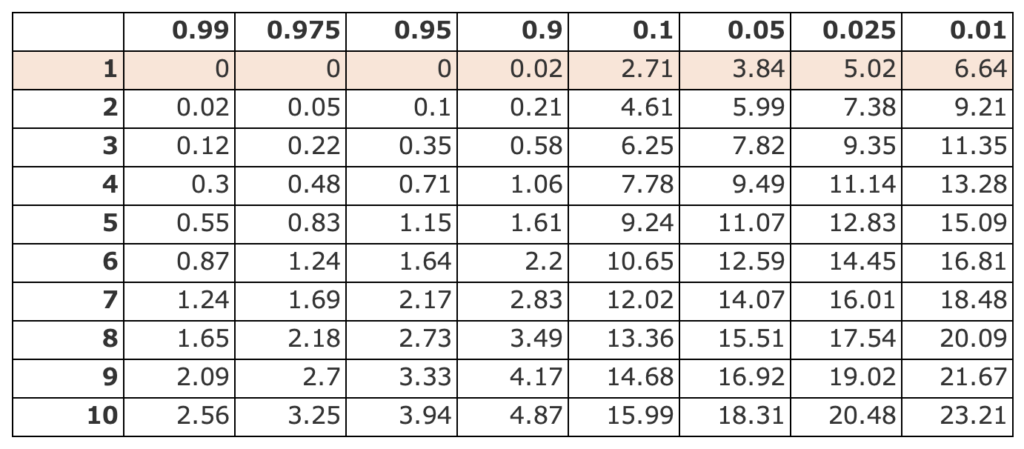
したがって、帰無仮説は有意水準10%で棄却されるが、5%で棄却されない(選択肢2)が正解になります。



