諸注意
- 問題本文は公式サイトまたは公式問題集を参照してください
- 統計検定2級に合格している方を想定して解説していきます
問題3-1 (1)
症例数が475件、帰無仮説がp = 0.05、対立仮説がp > 0.05の片側検定を行う。この時、帰無仮説の下で発現割合(母比率)が0.0733以上になる確率を求めよ。
選択肢
① 0.01 ② 0.025 ③ 0.05 ④ 0.1 ⑤ 0.2
答え ① 0.01
解説
前提知識
- 式1-1:二項分布
⇨ 母数のnは試行回数, pは成功確率を表す - 式1-2:正規分布
⇨ 母数の\(\mu\)は平均, \(\sigma^2\)は分散を表す - 式1-3:ラプラスの定理
⇨ 二項分布のn数が十分に大きい時、正規分布に近似する - 式1-4:標準化
⇨ Zスコアを変換する
式1
\begin{align}
& X \sim B(n, p) & (1) \\
& X \sim N(\mu, \sigma^2) & (2) \\
& B(n, p) \longrightarrow N(np, np(1-p)) & (3) \\
& Z = \text{(観測値}-\text{期待値) } / \text{ 標準偏差} & (4) \\
\end{align}
Zスコアの算出
式1より、症例数\(n\), 帰無仮説下での発現確率\(p\), 発現割合\(\hat{p}\)を用いてZスコアを求めます。
式2
\begin{align}
Z &= \frac{\text{観測値}-\text{期待値}}{\text{標準偏差}} = \frac{n\hat{p}-np}{\sqrt{np(1-p)}} = \frac{\hat{p}-p}{\sqrt{p(1-p)/n}}
\end{align}
問題文より、\(n=475\), \(p=0.05\), \(\hat{p} \geq 0.0733\)を代入します。
式3
\begin{align}
Z = \frac{\hat{p}-p}{\sqrt{p(1-p)/n}} = \frac{0.0733-0.05}{\sqrt{0.05(1-0.05)/475}} = 2.33 \\
\end{align}
標準正規分布の上側確率
式3の結果を用いて、付表1から対応する上側確率を探します。
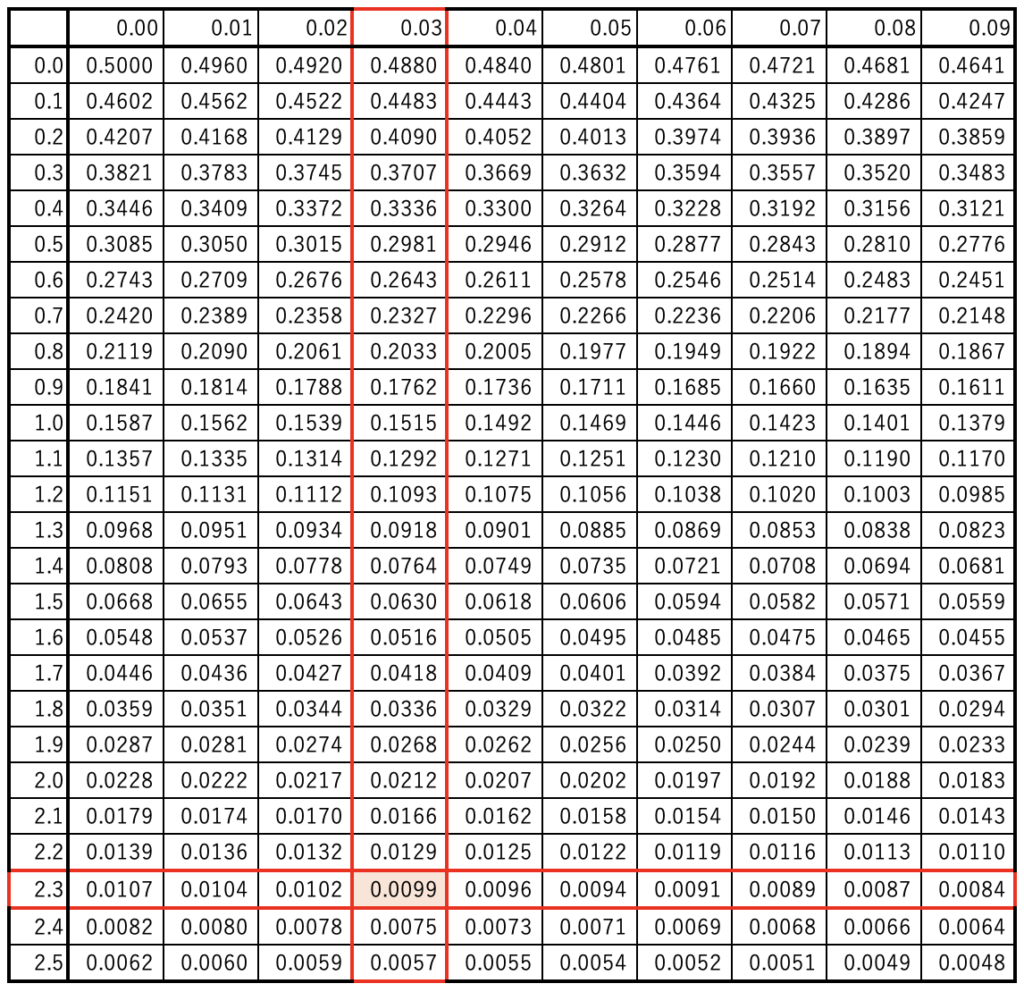
付表の結果より、発現割合が0.0733以上になる確率は0.01(選択肢①)になります。
問題3-1 (2)
帰無仮説がp = 0.05、対立仮説がp = 0.10の片側検定を行う。この時、有意水準が2.5%、検出力が90%になる症例数を答えよ。
選択肢
① 114 ② 164 ③ 214 ④ 264 ⑤ 314
答え ④ 264
解説
前提知識
検定とは、症例数・有意水準、検出力・効果量(帰無仮説と対立仮説の差)の4つの要素から成り立ちます。本問では既に『有意水準・検出力・効果量』が定まっているため、計算により適切な症例数が一意に定まります。
仮に計算を行わず、症例数に過不足がある場合は以下の不都合が生じます。
- (上) 症例数が少ない
帰無仮説と対立仮説の両方を棄却できない値が存在する - (中) 症例数が適正
帰無仮説と対立仮説のどちらかを常に棄却できる - (下) 症例数が多い
帰無仮説と対立仮説の両方を棄却してしまう値が存在する
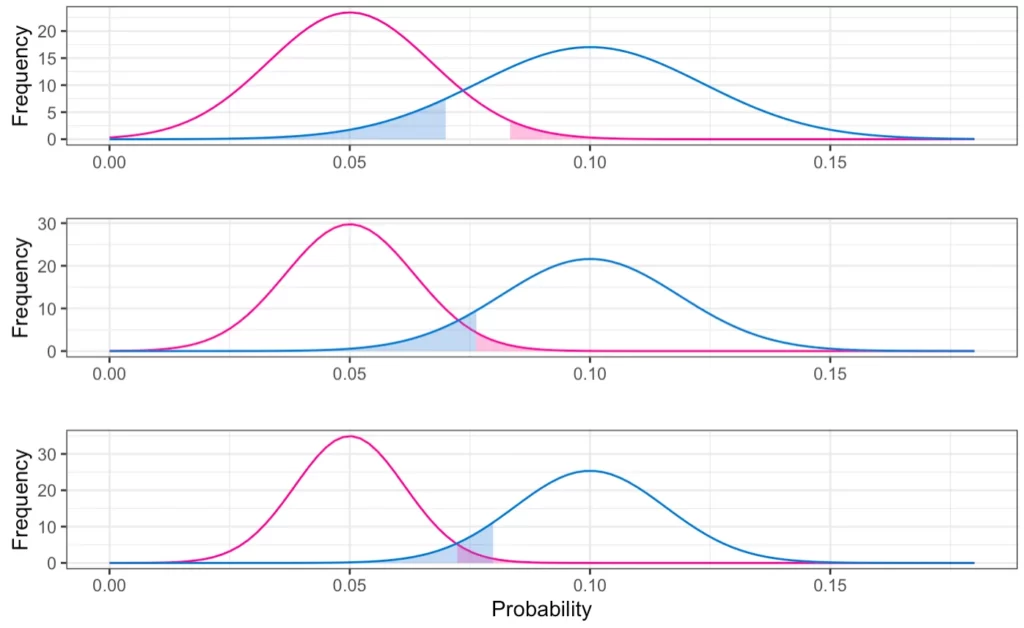
Zスコアの算出
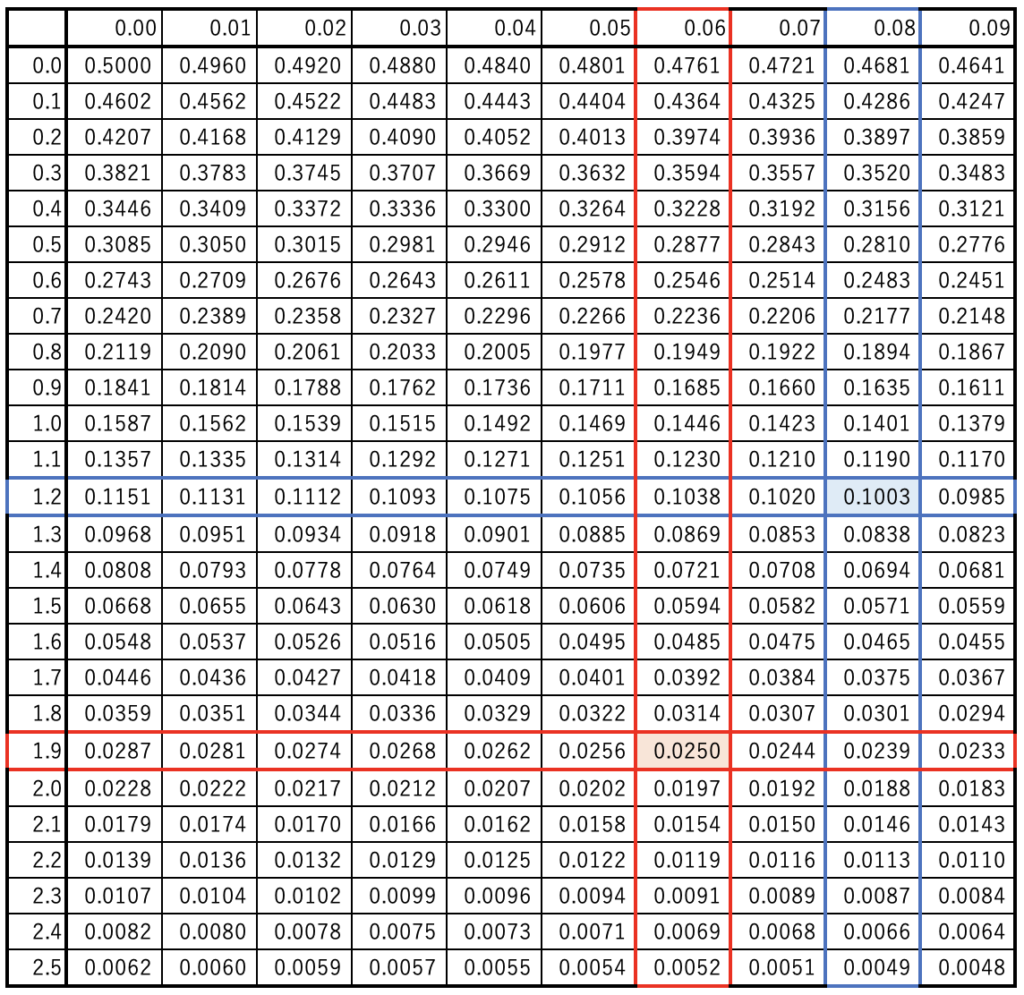
問題文より、第1種の過誤(有意水準)が\(\alpha = 0.025\), 第2種の過誤(1 – 検出力)が\(\beta = 1-0.90=0.100\)になるため、付表1から対応するZスコア探します。なお、第2種の過誤は下側確率を取るため、Zスコアがマイナスになる点に注意してください。
式4
\begin{align}
& \alpha=0.025=Q(1.96) \longrightarrow Z_0 = +1.96 & (1) \\
& \beta=0.100=Q(1.28) \longrightarrow Z_1 = -1.28 & (2) \\
\end{align}
症例数の計算
症例数を求めるため、先述の問題で使用したZスコアの算出式(式2)を用います。
式5(再掲)
\begin{align}
Z &= \frac{\hat{p}-p}{\sqrt{p(1-p) / n}}
\end{align}
帰無仮説下では、発現確率\(p_0=0.05\), \(Z_0=1.96\)を代入します。
式6(帰無仮説下)
\begin{align}
Z_0 &= \frac{\hat{p}-p_0}{\sqrt{p_0(1-p_0) / n}} \\
1.96 &= \frac{\hat{p}-0.05}{\sqrt{(0.05*0.95) / n}} \\
\hat{p} &= 0.05 + 1.96 \sqrt{\frac{(0.05*0.95)}{n}} \\
\end{align}
対立仮説下では、発現確率\(p_1=0.10\), \(Z_1=-1.28\)を代入します。
式7(対立仮説下)
\begin{align}
Z_1 &= \frac{\hat{p}-p_1}{\sqrt{p_1(1-p_1) / n}} \\
-1.28 &= \frac{\hat{p}-0.1}{\sqrt{(0.1*0.9) / n}} \\
\hat{p} &= 0.1 – 1.28 \sqrt{\frac{(0.1*0.9)}{n}} \\
\end{align}
式6, 7より、症例数nを求めます。
式8
\begin{align}
0.05 &+ 1.96 \sqrt{\frac{(0.05*0.95)}{n}} = 0.1 – 1.28 \sqrt{\frac{(0.1*0.9)}{n}} \\
\sqrt{n} &= \frac{1.96\sqrt{0.05*0.95}+1.28\sqrt{0.1*0.9}}{0.05} \\
\\
n &= 263.2 \\
\end{align}
したがって、適切な症例数は264(選択肢④)になります。
問題3-2 (1)
発現割合が0.05の有害事象が存在する。独立に8症例を調査したとき、有害事象が1例以上観測される確率を答えよ。
選択肢
① 0.05 ② 0.24 ③ 0.34 ④ 0.40 ⑤ 0.66
答え ③ 0.34
解説
有害事象が『1例以上観測される確率』の補事象は『1例も観測されない確率』になります。それぞれの症例で有害事象が発生しない確率は\(1 – 0.05 = 0.95\)です。8症例が独立であるため、有害事象が『1例も観測されない確率』は\(0.95^8=0.66\)になります。
ここから有害事象が『1例以上観測される確率』は\(1-0.66=0.34\)(選択肢③)になります。
問題3-2 (2)
発現割合が0.001の有害事象が存在する。1例以上観測される確率が0.95となる症例数を答えよ。なお、変数εが十分に小さい時に限り、\(ln(1-\epsilon)=-\epsilon\)を用いても良い。
選択肢
① 1,000 ② 1,500 ③ 2,000 ④ 2,500 ⑤ 3,000
答え ⑤ 3,000
解説
症例数を\(n\)、発現割合を\(\epsilon=0.001\)、1例以上観測される確率を\(p=0.95\)と置いた時、次の等式で表せます。
式9
\begin{align}
p &= 1 – (1-\epsilon)^n \\
\end{align}
試験では式9を電卓のみで解く必要があります。手間ですが、与えられたヒントと付表5(指数関数と常用関数)を用いて次のように症例数を求めます。
式10
\begin{align}
p &= 1 – (1-\epsilon)^n \\
0.95 &= 1-(1-0.001)^n \\
0.05 &= (1-0.001)^n \\
\ln(0.05) &= n\ln(1-0.001) \\
\ln(0.05) &= n\cdot -0.001 \\
n &= -1000 \cdot \ln(0.05) \\
n &= -1000 \cdot \ln(5) + \ln(0.01) \\
n &= -1000 \cdot (2.30\log(5) + 2.30\log(0.01)) \\
n &= -1000 \cdot (2.30*0.7 + 2.30*-2) \\
n &= 2990
\end{align}
したがって、症例数は3000(選択肢⑤)になります。



