諸注意
- 問題本文は公式サイトまたは公式問題集を参照してください
- 統計検定2級に合格している方を想定して解説していきます
問題6-1
文系が200名・理系が100名の計300名の学生が期末試験を受験した。文系と理系の点数は以下の正規分布(式1)に従い、混合正規分布で近似できる。この時、文系のAさんは64点・理系のBさんは86点であった。文系におけるAさんの偏差値と理系におけるBさんの偏差値を答えよ。
式1
\begin{align}
\text{文系}: N(65, 5^2) \\
\text{理系}: N(80, 3^2) \\
\end{align}
選択肢
① A: 29.4, B: 92.4
② A: 37.8, B: 92.0
③ A: 48.0, B: 70.0
④ A: 49.0, B: 72.7
⑤ A: 49.5, B: 63.5
答え ③ A: 48.0, B: 70.0
解説
前提知識
偏差値
試験結果(学力)が平均\(\mu\), 標準偏差\(\sigma\)の正規分布に従うと仮定する。これを標準化した後、平均を50, 標準偏差を10に変形したもの。
式2
\begin{align}
\frac{X-\mu}{\sigma} * 10 + 50
\end{align}
偏差値の計算
問題文より、文系のAさんと理系のBさんの点数と分布から偏差値を求めます。
- Aさん(文系)
⇨ 点数: 64点
⇨ 分布: \(N(65, 5^2)\) - Bさん(理系)
⇨ 点数: 86点
⇨ 分布: \(N(80, 3^2)\)
式3
\begin{align}
A = \frac{64-65}{5} * 10 + 50 = 48 \\
B = \frac{86-80}{3} * 10 + 50 = 70 \\
\end{align}
したがって、偏差値はAが48, Bが70になります。
問題6-2
文系と理系の混合正規分布として適切なグラフを答えよ。
答え 選択肢 ②(解説参照)
解説
前提知識
混合分布
2つ以上の確率分布が混合した分布。一般的に多峰性を持ちますが、確率分布の一種であることには変わりないため、取りやすい値の山が高くなります。
混合分布
期末試験の結果が、文系の学生は\(N(65, 5^2)\)に従い、理系の学生は\(N(80, 3^2)\)に従います。また、文系と理系の学生は比率が200対100になるため、文系のウェイトが高くなります。
ここから混合正規分布は以下のグラフの通りになります。
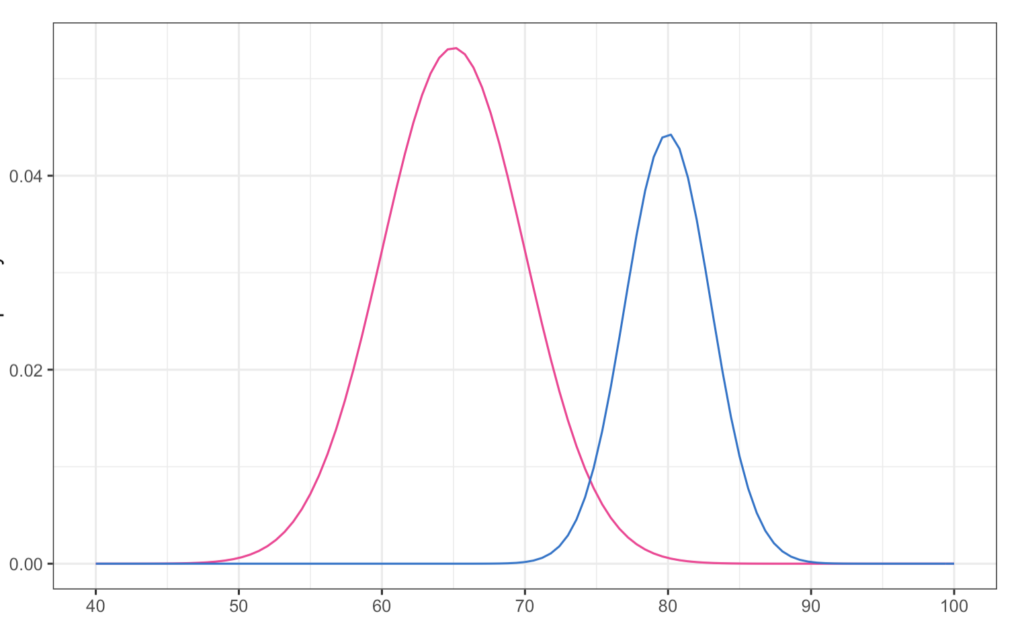
文系(赤色), 理系(青色)
したがって、選択肢②のグラフが正解になります。
問題6-3
期末試験で点数が60点以上の学生の数を答えよ。
選択肢
① 65% ② 70% ③ 80% ④ 90% ⑤ 98%
答え 選択肢 ④(90%)
解説
前提知識
正規分布の性質
平均を中心に標準偏差の2倍, 4倍, 6倍の幅に入るデータの割合は以下の通り
- 標準偏差の2倍 (\(-1\sigma \sim 1\sigma\))
⇨ 68.27% - 標準偏差の4倍 (\(-2\sigma \sim 2\sigma\))
⇨ 95.45% - 標準偏差の6倍 (\(-3\sigma \sim 3\sigma\))
⇨ 99.73%
標準化得点
文系と理系の学生がそれぞれ60点以上を取る確率を計算するため、まずは標準化した時の値(標準化得点)を計算します。
式4
\begin{align}
\text{文系} &= \frac{60-65}{5} = -1 \\
\text{理系} &= \frac{60-80}{3} = -6.67 \\
\end{align}
確率の計算
式4より、文系の学生が60点以上を取る確率\(P(-1 <= \sigma)\)を計算します。
式5
\begin{align}
&P(-1 <= \sigma) = P(-1 <= \sigma < 0) + P(0 <= \sigma) \\
\\
&P(-1 <= \sigma < 0) = 0.68/2 = 0.34 \\
&P(0 <= \sigma) = 0.5 \\
&P(-1 <= \sigma) = 0.34 + 0.5 = 0.84 \\
\end{align}
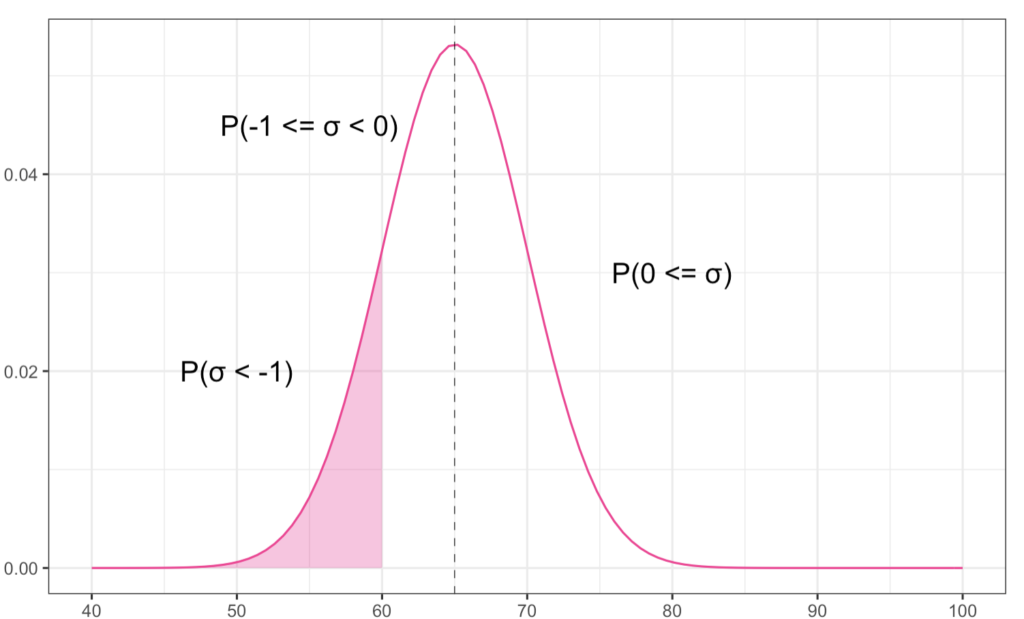
赤塗りの箇所は60点未満の学生を表す
文系の学生のうち、60点以上を取る人数は168名(=200×0.84)になります。また、理系の学生は計算するまでもなく、全員(100名)の学生が60点以上を取得しています。
ここから割合を計算します。
式6
\begin{align}
(168+100)/300 = 0.893
\end{align}
したがって、60点以上の学生の割合は90%になります。



