諸注意
- 問題本文は公式サイトまたは公式問題集を参照してください
- 統計検定2級の資格を持つ方を前提に解説していきます
問題8-1
\(u_1, u_2, …, u_T\)が式1(1次の自己回帰モデル AR(1))に従う。\(\alpha=0.5\)のAR(1)モデルに従うT=1000個の標本から求めた偏自己相関係数のプロットはどれか答えよ。
式1
\begin{align}
&u_{t+1} = \alpha u_t + \epsilon_{t+1} \\
\end{align}
\(|\alpha|<1, \epsilon \sim N(0, \sigma^2)\)に従い、\(u_1, u_2, …, u_T\)は定常であると仮定する
選択肢(割愛)
答え 選択肢 ②
解説
前提知識
自己相関係数
時系列データ内の特定の時点(例: 時点tと時点t+k)間の相関係数を表す。具体的には、本問でラグ2(\(u_{t+2}, u_t\))は\(u_{t+1}\)を通じて相関を持ちます。
式2
\begin{align}
&u_{t+2} = \alpha (\alpha u_t + \epsilon_{t+1}) + \epsilon_{t+2} \\
\end{align}
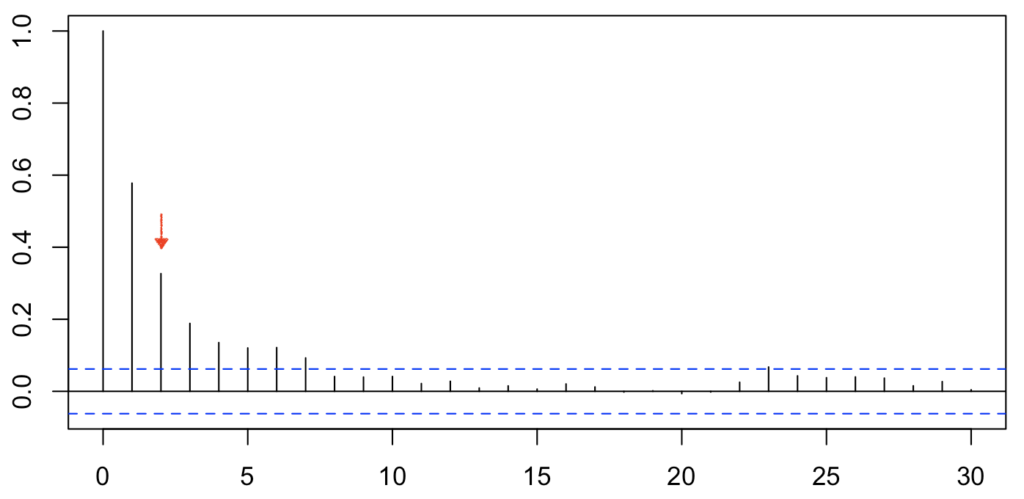
偏自己相関係数
自己相関係数は特定の時点以外(例: 時点t+s)の影響も受けるのに対して、偏自己相関係数は特定の時点以外の影響を取り除いた時の相関係数を表す。本問では、ラグ2(\(u_{t+2}, u_t\))は相関を持ちません。
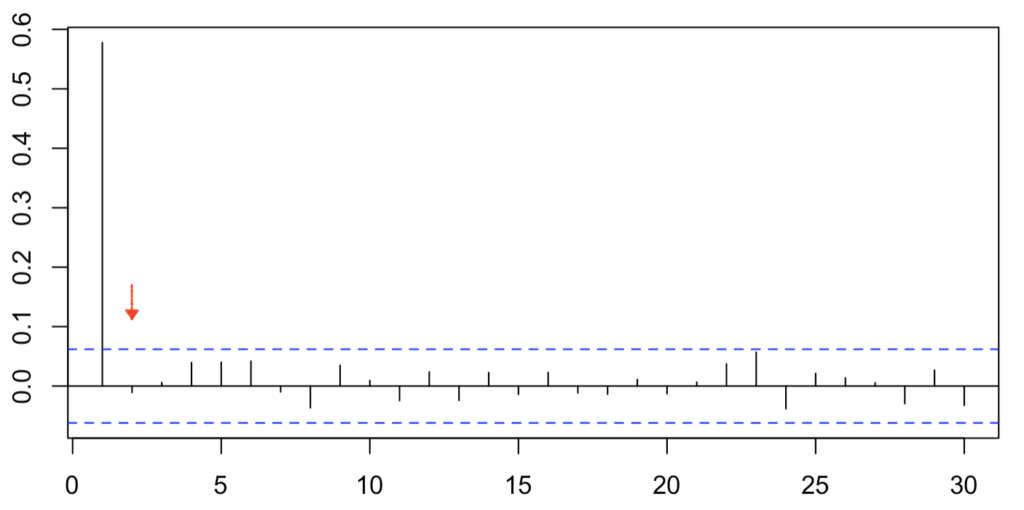
また、偏自己相関係数はラグ1以降の値に意味があり、ラグ0の相関が1であることが自明のため、R言語のpacf関数ではラグ0を描画しません。自己相関係数でも同じことが言えるのですが、そういう仕様らしいのでご注意ください。
相関係数
式1より、定常(\(|\alpha| < 1\))のAR(1)モデルは\(u_{t+1}\)が\(u_t\)の値に基づいて\(\alpha\)の比率で変化することを表しています。これは、線形関係の強さ(相関係数)を表しています。
式1(再掲)
\begin{align}
&u_{t+1} = \alpha u_t + \epsilon_{t+1} \\
\end{align}
また、AR(n)モデルでは、ラグn以降の時に偏自己相関が無相関になるという特徴があります。よって、AR(1)モデルでは相関が見られるのはラグ1のみになります。
したがって、選択肢②が正解になります。
問題8-2
\(\alpha=0.1\)のとき、\(u_t\)の分散\(\sigma_u^2\)を答えよ。
選択肢
① \(\sigma^2/0.9\) ② \(\sigma^2/0.99\) ③ \(\sigma^2\) ④ \(0.1\sigma^2\) ⑤ \(0.011\sigma^2\)
答え 選択肢 ②
解説
前提知識
定常性
時系列分析において重要な概念である定常性には、弱定常性と強定常性の二種類があります。一般的に時系列データの文脈で「定常」と言及される場合、弱定常性を指すことが多いです。弱定常性の時系列は以下の特性を持ちます。
- 平均の一定性:時系列データの平均(期待値)が時間に依存せず、一定であること
- 分散の一定性:時系列データの分散が時間に依存せず、一定であること
- 共分散の一定性:任意の二つの時点間の共分散が、それらの時点間の時間的な間隔のみに依存し、具体的な時点に依存しないこと
分散の計算
問題文より、\(u_t\)の分散が\(\sigma_u^2\)であり、\(\epsilon\)の分散が\(\sigma^2\)になります。また、(\(u_1, u_2, …, u_T\))は定常であるため、\(u_{t+1}\)の分散も\(\sigma_u^2\)になります。
式1(\(\alpha=0.1\))
\begin{align}
&u_{t+1} = 0.1 u_t + \epsilon_{t+1} \\
\end{align}
式3
\begin{align}
&V[u_{t+1}] = V[0.1 u_t] + V[\epsilon_{t+1}] \\
&\sigma_u^2 = 0.1^2\sigma_u^2 + \sigma^2 \\
&\sigma_u^2 = \sigma^2 / 0.99 \\
\end{align}
したがって、\(u_t\)の分散は\(\sigma_u^2 = \sigma^2/0.99\)になります。
問題8-3
(\(x_1, x_2, …, x_{10}\))は独立に同一の正規分布\(N(\mu, \sigma_u^2)\)に従い、平均は式4-1の通りである。また、(\(y_1, y_2, …, y_T\))は(\(y_t=\mu+u_t\))で求め、平均は式4-2の通りである。式1の\(\alpha\)が\(0<\alpha<1\)の時、\(\bar{x}, \bar{y}_T\)の2つの統計量の性質として正しいものと答えよ。
式1(再掲)
\begin{align}
&u_{t+1} = \alpha u_t + \epsilon_{t+1} \\
\end{align}
式4
\begin{align}
\bar{x} &= (1/10) \sum_{i=1}^{10} x_i & (1) \\
\bar{y}_T &= (1/T) \sum_{t=1}^T y_t & (2) \\
\end{align}
選択肢
① \(\bar{x}, \bar{y}_T\)ともに不偏であり、\(T=10\)の時は\(\bar{x}, \bar{y}_{10}\)の分散は等しい
② \(\bar{y}_{T}\)には偏りがあるが、\(T=10\)の時は\(\bar{x}, \bar{y}_{10}\)の分散は等しい
③ \(\bar{x}, \bar{y}_T\)ともに不偏であるが、\(T=10\)の時は\(\bar{x}\)の方が\(\bar{y}_{10}\)の分散より小さい。\(\bar{y}_T\)が\(\bar{x}\)より小さい分散を得るためには\(T>10\)の標本が必要になる
④ \(\bar{x}, \bar{y}_T\)ともに不偏である。\(T=10\)の時の\(\bar{x}\)の分散と\(\bar{y}_{10}\)の分散の大小関係は\(\alpha\)の値に依存する。つまり、\(\alpha\)の値によっては\(\bar{x}\)よりも\(\bar{y}_{10}\)の方が、\(\mu\)の推定量として精度が良くなることがあり得る
⑤ \(\bar{y}_{T}\)には偏りがあるが、\(T=10\)の時は\(\bar{y}_{10}\)の方が\(\bar{x}\)の分散よりも小さい
答え 選択肢 ③
解説
前提知識
AR(1)の期待値
AR(1)が定常(\(|a|<1\))であり、ホワイトノイズ\(\epsilon\)の平均が0の時、以下の式を\(\alpha\)の値に関わらず満たすためには、\(E[u]=0\)である必要があります。
式5
\begin{align}
&E[u_{t+1}] = E[\alpha u_t + \epsilon_{t+1}] \\
&E[u_{t+1}] = E[\alpha u_t] + E[\epsilon_{t+1}] \longleftarrow E[\epsilon_{t+1}]=0 \\
&E[u_{t+1}] = \alpha E[u_t] \longleftarrow \text{定常性: } E[u_{t+1}] = E[u_t] \\
&E[u] = \alpha E[u] \\
\end{align}
分散の公式
分散は以下の式を用いて計算することができます。また、期待値\(E[X]\)が0の時、\(V[X]=E[X^2]\)となる性質は頻出するため、覚えておくと便利です。
式6
\begin{align}
&V[X] = E[X^2] – E[X]^2 \\
\end{align}
\(\bar{y}_T\)の不偏性
\(\bar{y}_T\)は\(y_t=\mu+u_t\)の平均であり、\(u_t\)は定常なAR(1)に従います。この時、\(y_t, \bar{y}_T\)の期待値は以下の通り求めることができます。
式7
\begin{align}
&E[y_t] = E[\mu+u_t] \\
&E[y_t] = \mu + E[u_t] \longleftarrow E[u_t] = 0\\
&E[y_t] = \mu \\
\end{align}
式8
\begin{align}
&E[\bar{y}_T] = E\left[\frac{1}{T} \sum_{t=1}^{T} y_t \right] = \frac{T}{T} E[y_t] = \mu \\
\end{align}
ここから\(\bar{y}_T\)は\(\mu\)の不偏推定量であることが分かるため、選択肢②と⑤が正しくないことが分かります。
\(\bar{x}\)の分散
\(x_i\)は独立に正規分布\(N(\mu, \sigma_u^2)\)に従う標本であり、\(\bar{x}\)はその平均です。この場合、平均\(\bar{x}\)の分散は元の分布の分散をサンプルサイズで割った値と一致します。
式9
\begin{align}
&V[\bar{x}] = \frac{\sigma_u^2}{n} = \frac{\sigma_u^2}{10} \\
\end{align}
\(\bar{y}_T\)の分散
まずは、\(u_{t+1}\)の分散を公式(\(V[u_{t+1}]=E[u_{t+1}^2]-(E[u_{t+1}])^2\))を用いて求めます。ただし、\(E[u_{t+1}]=0\)であることが既に分かっているため、\(V[u_{t+1}]\)は\(E[u_{t+1}^2]\)と等しくなります。
式10
\begin{align}
V[u_{t+1}] &= E[u_{t+1}^2] \\
&= E[(\alpha u_t + \epsilon_{t+1})^2] \\
&= E[\alpha^2 u_t^2 + 2\alpha u_t \epsilon_{t+1} + \epsilon_{t+1}^2] \\
&= E[\alpha^2 u_t^2] + E[2\alpha u_t \epsilon_{t+1}] + E[\epsilon_{t+1}^2] \longleftarrow E[\epsilon_{t+1}]=0, E[\epsilon_{t+1}^2]=V[\epsilon_{t+1}]=\sigma^2 \\
&= \alpha^2 E[u_t^2] + \sigma_u^2 \longleftarrow V[u_{t}]=E[u_{t}^2] \\
&= \alpha^2 V[u_t] + \sigma_u^2 \longleftarrow V[u_{t+1}]=V[u_t] \\
\\
V[u] &= \alpha^2 V[u] + \sigma_u^2 \\
&= \frac{\sigma_u^2}{1-\alpha^2} \\
\end{align}
次に、\(y_t\)の分散を求めます。問題文より(\(y_t=\mu+u_t\))になります。
式11
\begin{align}
V[y_t] &= E[y_t^2] – E[y_t]^2 \\
&= E[(\mu+u_t)^2] – E[\mu+u_t]^2 \\
&= E[\mu^2+2\mu u_t+u_t^2] – E[\mu+u_t]^2 \\
&= \mu^2+2\mu E[u_t]+E[u_t^2] – (\mu+E[u_t])^2 \longleftarrow E[u_t]=0, E[u_t^2]=V[u_t]=\frac{\sigma_u^2}{1-\alpha^2} \\
&= \mu^2 + \frac{\sigma_u^2}{1-\alpha^2} – \mu^2 \\
&= \frac{\sigma_u^2}{1-\alpha^2} \\
\end{align}
次に、\(\bar{y}_T\)の分散を求める必要がありますが、互いに相関を持つ(\(y_1, y_2, …, y_T\))は計算が複雑になるため、試験時間中に解くことが現実的ではありません。
選択肢の間違え探し
\(\bar{x}, \bar{y}_T\)がともに不偏としている選択肢は1, 3, 4になります。そのため、不偏以外の箇所を見て、正しい選択肢を見つけていきます。
① \(T=10\)の時は\(\bar{x}, \bar{y}_{10}\)の分散は等しい
⇨ それぞれ構成する値の分散が\(V[x]=\sigma_u^2\)と\(V[y_t]=\frac{\sigma_u^2}{1-\alpha^2}\)になるため、\(\bar{x}\)と\(\bar{y}_{10}\)の分散は等しくない
③ \(T=10\)の時は\(\bar{x}\)の方が\(\bar{y}_{10}\)の分散より小さい。\(\bar{y}_T\)が\(\bar{x}\)より小さい分散を得るためには\(T>10\)の標本が必要になる
⇨ \(V[y_t]=\frac{\sigma_u^2}{1-\alpha^2}\)は\(0<\alpha\)の時、\(V[x]<V[y_t]\)になる。また、サンプルサイズが増えると分散が小さくなる
④ \(T=10\)の時の\(\bar{x}\)の分散と\(\bar{y}_{10}\)の分散の大小関係は\(\alpha\)の値に依存する。つまり、\(\alpha\)の値によっては\(\bar{x}\)よりも\(\bar{y}_{10}\)の方が、\(\mu\)の推定量として精度が良くなることがあり得る
⇨ \(V[y_t]=\frac{\sigma_u^2}{1-\alpha^2}\)は\(\alpha\)によって値が変化するが、\(0<\alpha\)の時は\(V[x]<V[y_t]\)になるため、\(\bar{x}\)よりも\(\bar{y}_{10}\)の方が\(\mu\)の推定量として精度が良くなることはない
したがって、選択肢③が正解になります。



