諸注意
- 問題本文は公式サイトまたは公式問題集を参照してください
- 統計検定2級の資格を持つ方を前提に解説していきます
問題4-1
あるアプリの男女別の利用数が以下のクロス表の通りだった。これをグラフ化したモザイクプロットを答えよ。
| 利用している | 利用していない | 計 | |
| 20代男 | 38 | 73 | 111 |
| 20代女 | 60 | 46 | 106 |
| 計 | 98 | 119 | 217 |
答え 選択肢①
解説
クロス表の変形
クロス表を男女別の割合に直し、モザイクプロットと併せてクロス表を変形します。
| 20代女 | 20代男 | |
| 利用していない | 43.40% | 65.77% |
| 利用している | 56.60% | 34.23% |
クロス表と一致するプロットは以下の形になります。
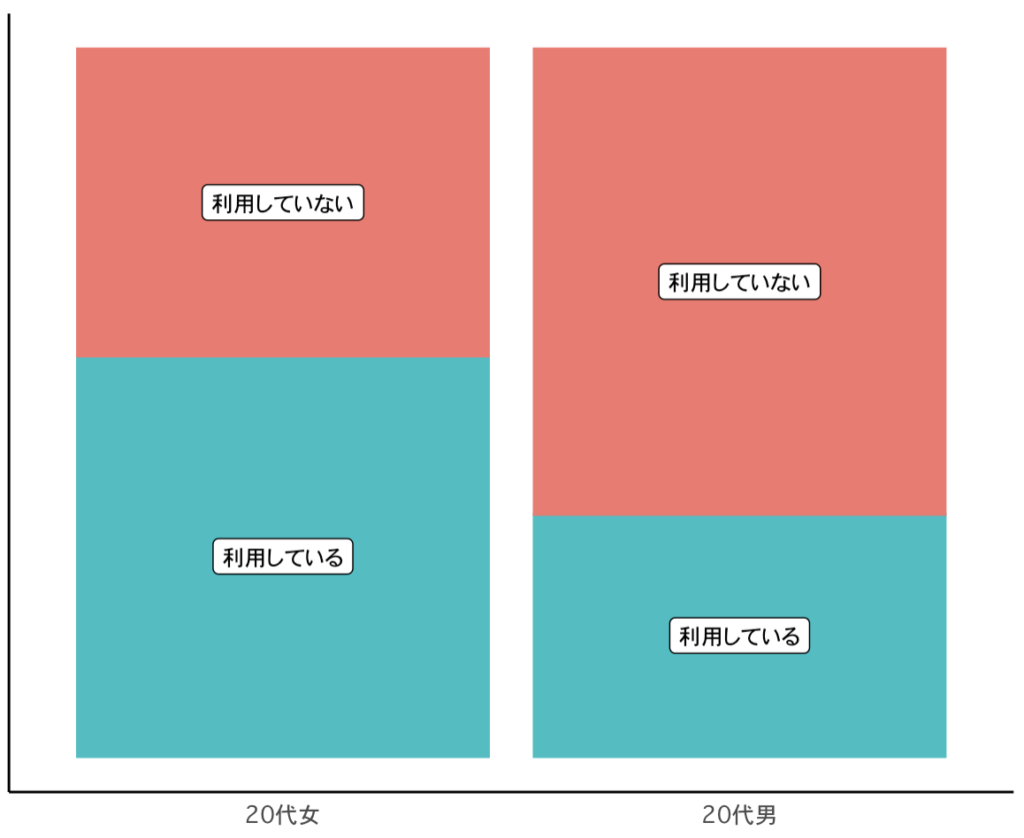
したがって、選択肢①が正解になります。
問題4-2
利用率に男女差がないという帰無仮説に対する両側検定を行う。検定統計量Zの絶対値が\(z_{a/2}\)よりも大きければ有意差ありとみなす時、統計検定量Zとして適切なものを答えよ。
答え \(Z=\frac{38/111-60/106}{\sqrt{(1/111+1/106) \cdot (98/217) \cdot (119/217)}}\)
解説
前提知識
2標本検定
2標本間の差の有無を検定する手法。2標本間の差が特定の確率分布(標準正規分布など)に従うと仮定し、観測されたデータが偶然によるものかどうかを数値的に評価します。
検定統計量Zが期待値0, 分散1の標準正規分布に従うと仮定する場合、2標本間の差を標準化するため、標準誤差(標準偏差の推定値)で割って計算します。
- \(\hat{p}_a\): 標本Aの割合の推定値
- \(\hat{p}_b\): 標本Bの割合の推定値
- \(\hat{p}\): 標本全体の割合の推定値
- \(n_a\): 標本Aのサンプルサイズ
- \(n_b\): 標本Bのサンプルサイズ
式1
\begin{align}
Z = \frac{\hat{p}_a – \hat{p}_b}{\sqrt{\hat{p}(1-\hat{p})(\frac{1}{n_a}+\frac{1}{n_b})}} \\
\end{align}
クロス表(再掲)
| 利用している | 利用していない | 計 | |
| 20代男 | 38 | 73 | 111 |
| 20代女 | 60 | 46 | 106 |
| 計 | 98 | 119 | 217 |
2標本検定
本問では標本A, Bが男女のアプリ利用数になります。ここから各値は以下の通りであり、検定統計量Zを計算します。
- \(\hat{p}_a\): 男性の利用率の推定値
⇨ \(\frac{38}{111}\) - \(\hat{p}_b\): 女性の利用率の推定値
⇨ \(\frac{60}{106}\) - \(\hat{p}\): 全体の利用率の推定値
⇨ \(\frac{98}{217}\) - \(n_a\): 男性のサンプルサイズ
⇨ 111 - \(n_b\): 標本Bのサンプルサイズ
⇨ 106
式2
\begin{align}
Z = \frac{\frac{38}{111}-\frac{60}{106}}{\sqrt{\frac{98}{217}(1-\frac{98}{217})(\frac{1}{111}+\frac{1}{106})}} \\
\end{align}
したがって、\(Z=\frac{38/111-60/106}{\sqrt{(1/111+1/106) \cdot (98/217) \cdot (119/217)}}\)



