諸注意
- 問題本文は公式サイトまたは公式問題集を参照してください
- 統計検定2級の資格を持つ方を前提に解説していきます
問題3-1
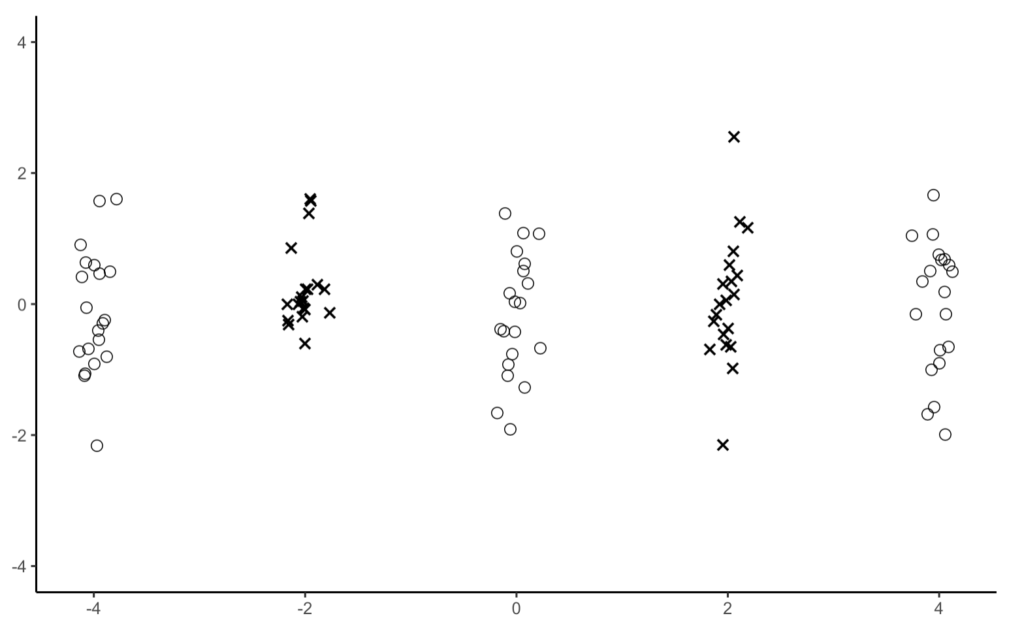
正例(+1)と負例(-1)の2群からなる2次元データが図1の散布図のように分布している。正例と負例を判別するため、p次の多項式カーネル(式1)を用いて、SVMで判別を行う。この時、正しく判別するために必要な最小の次数pを答えよ。
図1
式1
\begin{align}
& k(x, x’) = (1+x^Tx’)^p \\
\end{align}
答え 4
解説
前提知識
多項式カーネル
データの特徴をより高次元の空間に写像することで線形分離を可能にする手法、またはその計算式を指します。計算式に含まれる\(x^Tx’\)はxとx’の内積を表しており、内積はベクトル間の類似度や相関を数値化する手法として使用されます。
2次以上の方程式を表す際、平面上では曲線になりますが、多次元においては直線で表すことが可能になります。直線で表すために必要な次数は方程式の次数と一致します。
SVM(サポートベクターマシーン)
多次元上でデータのグループを最もうまく分ける線を見つけ出すための手法になります。本問では重要なワードではないため、問題3-2で改めて解説します。
グラフから読み取る
図1から正例はX軸の(-4, 0, 4)付近に集中しており、負例はX軸の(-2, 2)付近に集中していることが分かります。ここからX軸の(-3, -1, 1, 3)付近に境界線を設けることでデータをうまく分離できそうです。
実際に4次方程式\((y = (x-3)(x-1)(x+1)(x+3))\)を当てはめたところ、以下の通りデータをうまく分離することができました。
図2
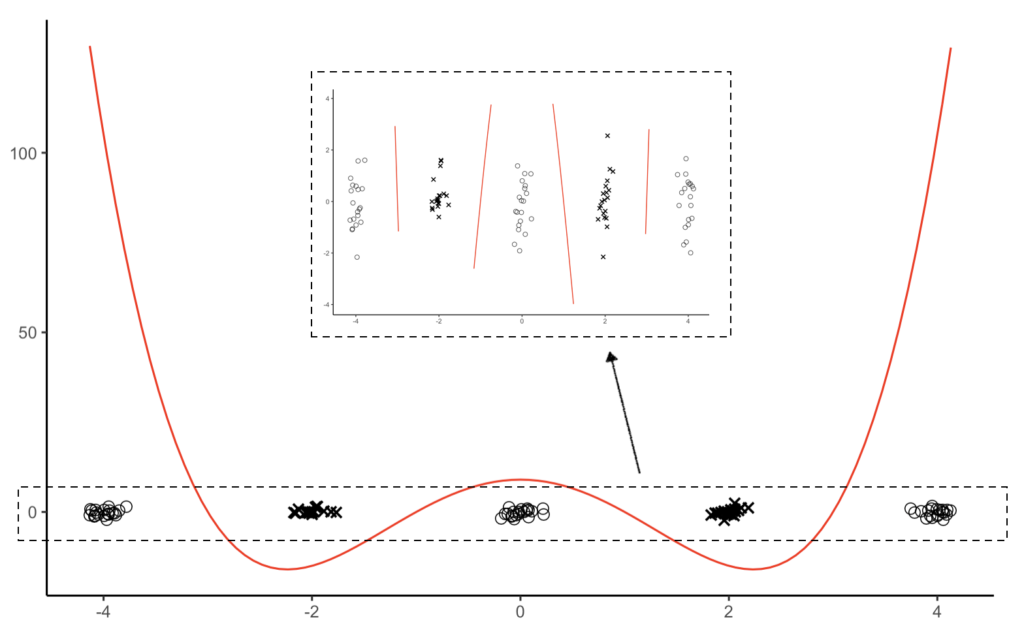
したがって、判別に必要な最小の次数は4になります。
問題3-2
正例と負例の2群からなる2次元データが図3の散布図のように分布している。正例と負例を判別するため、「ソフトマージンSVM」と「線形判別分析」の2つの手法を適用する。
まず、全てのデータに対して2つの手法で判別分析を行う。その後、得られた判別直線に近い観測値のみを残して再び2つの手法で判別分析を行ったところ、ソフトマージンSVMの結果が全く変化しなかった。その理由を答えよ。
図3
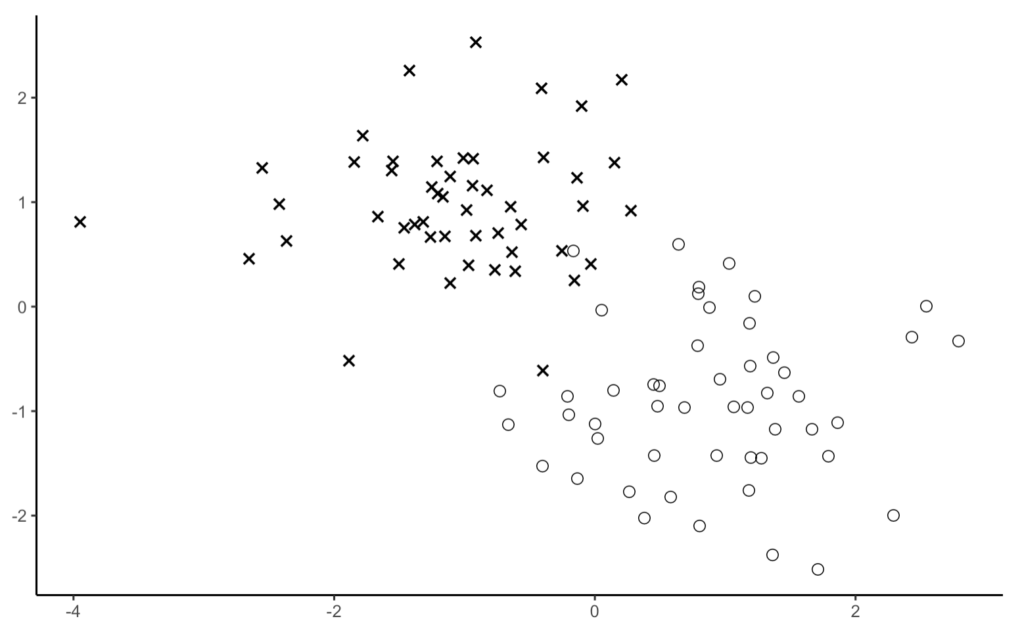
答え SVMの判別直線はサポートベクターにのみ依存するため
解説
前提知識
SVM(サポートベクターマシーン)
サポートベクター(分類線に最も近い観測値)にのみ依存して判別直線を定める手法。誤判定を防ぐ(マージンを最大化する)ため、サポートベクターから最も離れた位置に判別直線を定める。
ソフトマージンSVM
誤判定を許さないSVMを『ハードマージンSVM』と呼ぶのに対して、ある程度の誤判定を許容する手法。本問では重要なワードではないため、数式は割愛します。
線形判別分析
全ての観測値を用いて、グループ間の違いを最大にし、グループ内の違いを最小にする判別直線を定める手法。
SVMの特徴
サポートベクター以外の点は判別直線の位置に影響を与えません。今回の問題文にある「判別直線に近い観測値のみを残して」という操作は、まさにサポートベクターを残すことに他ならず、他の点は無視されるため、SVMの判別直線は変化しません。
したがって、SVMの判別直線はサポートベクターにのみ依存するため結果が変化しない



