諸注意
- 問題本文は公式サイトまたは公式問題集を参照してください
- 統計検定2級の資格を持つ方を前提に解説していきます
問題10-1
日本の1741市町村について、ふるさと納税による寄付金額の要因を分析するための重回帰分析を行う。この時、被説明変数と説明変数は以下の通りであり、重回帰分析は式1のモデルで表される。
- \(y_i\): 寄付金額
- \(x^{(1)}_{i}\): 人口
- \(x^{(2)}_{i}\): 返礼品の種類数(最大166)
- \(x^{(k)}_{i}\): 166品目の返礼品の取り扱いの有無(ダミー変数)
⇨ (\(k=3, 4, …, 168\))
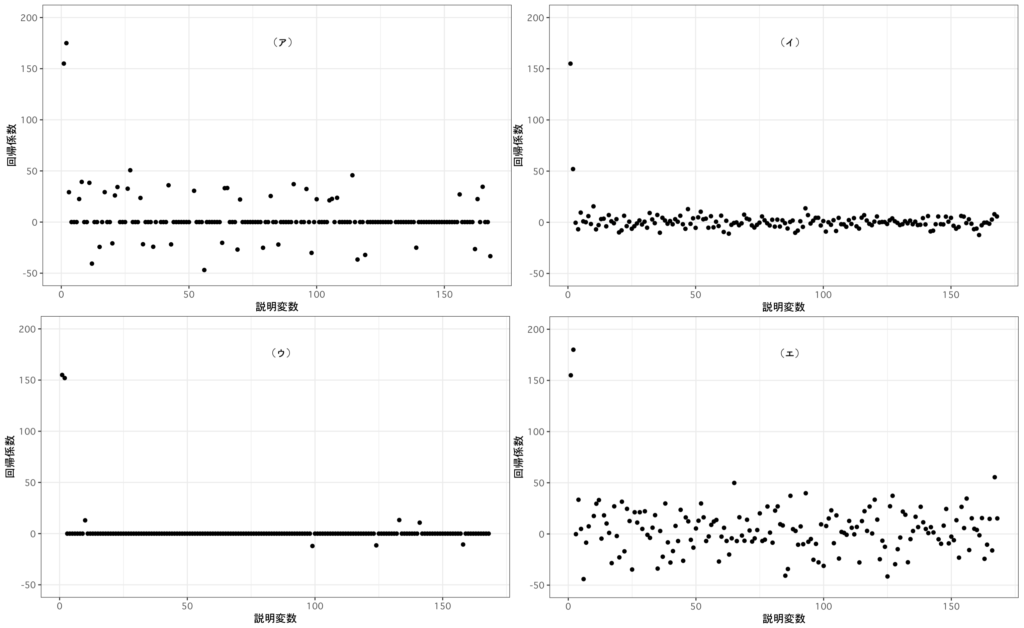
このモデルの推定には、最小二乗法(OLS法), OLS法 + AIC, L1正則化法, L2正則化法の4つの方法を用いた。なお、正則化法(\(q=1,2\))は式2のモデルで表される。この時、「推定法」と「各推定法における回帰係数の推定値と説明変数のプロット」の組み合わせとして適切なものを答えよ。
式1
\begin{align}
y_i=\beta_0 + \sum_{k=1}^{168} \beta_k x^{(k)}_{i} + u_i \\
\end{align}
\(u_i\)は誤差項を表す
式2
\begin{align}
\sum_{i=1}^{1741} \left(y_i-\left(\beta_0+\sum_{k=1}^{168} \beta_k x^{(k)}_{i}\right)\right)^2 + \lambda \sum_{k=1}^{168} |\beta_k|^q \\
\end{align}
\(\lambda\)は正則化パラメータを表す
選択肢
① (ア) OLS法, (イ) L1正則化法, (ウ) OLS法 + AIC, (エ) L2正則化法
② (ア) OLS法, (イ) OLS法 + AIC, (ウ) L1正則化法, (エ) L2正則化法
③ (ア) L2正則化法, (イ) OLS法 + AIC, (ウ) L1正則化法, (エ) OLS法
④ (ア) OLS法, (イ) L2正則化法, (ウ) L1正則化法, (エ) OLS法 + AIC
⑤ (ア) OLS法 + AIC, (イ) L2正則化法, (ウ) L1正則化法, (エ) OLS法
答え 選択肢 ⑤
解説
前提知識
最小二乗法(OLS法)
観測値から適切な線形モデルを求める手法であり、データに対するモデルの予測値と観測値の差(残差)の二乗和が最小になる組み合わせを計算します。目的関数は式3の通りです。
最小二乗法はモデルの予測精度のみに焦点を当てており、回帰係数の大きさは直接的には考慮されません。
式3
\begin{align}
&\sum_{i=1}^{n} (y_i – \hat{y})^2 \\
\end{align}
L2正則化法
最小二乗法と同じ目的で使われますが、正則化項の有無に違いがあります。L2正則化法では回帰係数の二乗値に罰則を課しており、目的関数は式4の通りです。
正則化項が加わることにより、最小二乗法と比較して回帰係数の絶対値を小さく保つことができます。
式4
\begin{align}
&\sum_{i=1}^{n} (y_i – \hat{y})^2 – \lambda \sum_{j=1}^{p} \beta_j^2\\
\end{align}
L1正則化法
L2正則化法と同じ目的で使われますが、回帰係数の絶対値に罰則を課しており、変化の小さい箇所を0に丸める性質(スパース性)を持ちます。目的関数は式5の通りです。
式5
\begin{align}
&\sum_{i=1}^{n} (y_i – \hat{y})^2 – \lambda \sum_{j=1}^{p} |\beta_j|\\
\end{align}
グラフの傾向
問題文より、各グラフの特徴を読み取ります。

| (ア)回帰係数の分散が大きい + スパース性あり | (イ)回帰係数の分散が小さい + スパース性なし |
| (ウ)回帰係数の分散が小さい + スパース性あり | (エ)回帰係数の分散が大きい + スパース性なし |
回帰係数の分散が(最小二乗法と比較して)小さいのは、正則化法の特徴になります。そのため、(イ)と(ウ)が正則化法であることが分かります。また、(イ)と(エ)はスパース性を持ちません。
ここから(イ)がL2正則化法、(ウ)がL1正則化法、(エ)が最小二乗法になります。消去法で(ア)が最小二乗法+AICになります。
したがって、選択肢⑤が正解になります。
問題10-2
ElasticNet回帰法を用いて推定を行う。ElasticNet回帰法のモデルは式6の通りであり、\(\alpha=1\)の時はL1正則化法、\(\alpha=0\)の時はL2正則化法と一致する。
\(\alpha\)を(0.0, 0.5, 0.7, 1.0)にそれぞれ固定した場合、\(log(\lambda)\)の値が(2, 4, 6)の時の回帰係数の推定値が非ゼロになる説明変数の数が選択肢のいずれかになった。\(\alpha=0.5\)の時の選択肢を答えよ。
式6
\begin{align}
&\sum_{i=1}^{1741} \left(y_i-\left(\beta_0 + \sum_{k=1}^{168} \beta_k x_{i}^{(k)} \right)\right)^2 + \lambda \sum_{k=1}^{168} \left( \alpha |\beta_k| + (1-\alpha) |\beta_k|^2 \right)
\end{align}
選択肢
① \(log(2)=127, log(4)=13, log(6)=1\)
② \(log(2)=98, log(4)=3, log(6)=0\)
③ \(log(2)=168, log(4)=168, log(6)=168\)
④ \(log(2)=109, log(4)=10, log(6)=0\)
答え 選択肢 ①
解説
正則化項
\(log(\lambda)\)の値が大きいほど、正則化項のウェイトが大きくなります。正則化項のウェイトが大きくなるほどスパース性を完全に持たないL2正則化法(\(\alpha=0\))以外では、回帰係数の推定値が0になる説明変数の数が増加します。
本問の選択肢では、回帰係数の推定値が0(非ゼロではない)になる説明変数の数が(③ < ① < ④ < ②)の順になります。これは\(\alpha\)の値(0.0 < 0.5 < 0.7 < 1.0)と一致します。
したがって、\(\alpha=0.5\)は選択肢①になります。



