諸注意
- 問題本文は公式サイトまたは公式問題集を参照してください
- 統計検定2級の資格を持つ方を前提に解説していきます
問題9-1
クロス集計表の各セルの頻度をa倍(a=2, 3, …)とした時、ピアソンのカイ二乗統計量、カイ二乗検定のP値、クラメールの連関係数(式1)の値の関係として適切なものを答えよ。
式1
\begin{align}
V=\sqrt{\frac{\chi^2}{n * (k-1)}}
\end{align}
\(\chi^2\)はカイ二乗統計量, nは標本サイズ, kはクロス集計表の行数と列数の大きくない方を表す
選択肢
① カイ二乗統計量, P値, 連関係数は全て大きくなる
② カイ二乗統計量, P値, 連関係数は全て変わらない
③ カイ二乗統計量は大きくなるが, P値と連関係数は小さくなる
④ カイ二乗統計量は大きくなり, P値は小さくなるが, 連関係数は変わらない
⑤ カイ二乗統計量と連関係数は大きくなるが、P値は小さくなる
答え 選択肢 ④
解説
前提知識
ピアソンのカイ二乗検定
2つのカテゴリ(年代と利用メディアなど)が無相関であると仮定した時の頻度と観測頻度を比較して、偶然の度合いを調べる検定手法。カイ二乗統計量\(\chi^2\)と自由度\(\nu\)を計算し、カイ二乗分布表を用いて有意度を求めます。
式2
\begin{align}
&\chi^2 = \sum (\text{観測頻度} – \text{期待頻度})^2 / \text{期待頻度} \\
&\nu = (\text{行数} – 1) \cdot (\text{列数} – 1) \\
\end{align}
自由度が同じ場合、カイ二乗統計量が大きいほどP値は小さくなります。
クラメールの連関係数
ピアソンのカイ二乗検定に基づき、二つの変数間の関連の強さを測定するための指標。相関係数と似た性質を持ちますが、以下の違いがあります。
- 代表
⇨ 相関係数:ピアソンの相関係数
⇨ 連関係数:クラメールの連関係数 - 定義
⇨ 相関係数:2つの量的データの線形関係の強さを測定する
⇨ 連関係数:2つの質的データの関連の強さを測定する - 値
⇨ 相関係数:-1(完全な負の相関) 〜 0(無相関) 〜 1(完全な正の相関)
⇨ 連関係数:0(全く関連がない) 〜 1(完全な関連)
値の変化
観測頻度が増えるほど、ピアソンのカイ二乗統計量は増加する傾向があります。例えば、観測頻度が10, 期待頻度が5の時、以下の通り変化します。
式3
\begin{align}
&\chi^2=(aX – a\bar{X})^2 / a\bar{X} \\
\\
&f(a=1) = (10 – 5)^2 / 5 = 5 \\
&f(a=2) = (20 – 10)^2 / 10 = 10 \\
&f(a=3) = (30 – 15)^2 / 15 = 15 \\
\end{align}
また、自由度が同じ場合、P値はカイ二乗統計量の増加と反比例して減少します。
次にクラメールの連関係数は、観測頻度の増減では変化しません。例えば、標本サイズが500, 行数が2の時、以下の通り変化します。
式4
\begin{align}
&V=\sqrt{\frac{\chi^2}{an * (k-1)}} \\
\\
&f(a=1)=\sqrt{\frac{5}{500}} = 0.1 \\
&f(a=2)=\sqrt{\frac{10}{1000}} = 0.1 \\
&f(a=3)=\sqrt{\frac{15}{1500}} = 0.1 \\
\end{align}
したがって、各セルの頻度がa倍になった時、カイ二乗統計量は大きく, P値は小さくなり、連関係数の値は変化しません。
問題9-2
年代と最も利用するメディアの関係を調べた結果、以下のクロス表が得られた。この時、選択肢の中から適切なものを答えよ。なお、標本サイズが1500, カイ二乗統計量の値は116.52であった。
| テレビ | ラジオ | 新聞 | 雑誌 | 書籍 | インターネット | その他 | |
| 10代 | 94 | 2 | 15 | 0 | 4 | 23 | 1 |
| 20代 | 106 | 3 | 41 | 0 | 2 | 64 | 3 |
| 30代 | 133 | 2 | 53 | 1 | 6 | 73 | 7 |
| 40代 | 186 | 3 | 55 | 1 | 3 | 56 | 6 |
| 50代 | 157 | 6 | 67 | 0 | 1 | 24 | 2 |
| 60代 | 203 | 7 | 69 | 1 | 4 | 15 | 1 |
選択肢
① クラメールの連関係数の値が0.1程度であるので、年代とメディアの間に強い関係があるかどうかは疑わしい。ピアソンのカイ二乗検定のP値が1%未満なのは標本サイズが大きいためである。
② クラメールの連関係数の値が0.1程度なので、標本サイズが大きいが、年代とメディアの間には実質的に有意な関係があると言える。
③ クラメールの連関係数の値が0.5程度なので、年代とメディアの間には中程度の関係があるといえる。
④ ピアソンのカイ二乗検定のP値は1%未満であるから、年代とメディアの間には強い関係があると言える。
⑤ ピアソンのカイ二乗検定は5%有意ではなく、クラメールの連関係数の値も0.1程度であることから、年代とメディアの間の関係の有無に関する情報を得ることはできない。
答え 選択肢 ①
解説
連関係数の計算
問題文より、標本サイズnが1500, カイ二乗統計量\(\chi^2\)が116.52, 列数と行数が7×6のクロス表になるため、式1に値を代入して計算します。
式5
\begin{align}
V&=\sqrt{\frac{\chi^2}{n * (k-1)}} \\
&=\sqrt{\frac{116.52}{1500 * (6-1)}} \\
&=0.12 \\
\end{align}
P値の計算
7×6のクロス表になるため、自由度は\(((7-1) \cdot (6-1) = 30)\) になります。カイ二乗分布表から自由度30の上側1%点は50.89になるため、\(\chi^2=116.52\)のP値は1%未満になります。
選択肢
① クラメールの連関係数の値が0.1程度であるので、年代とメディアの間に強い関係があるかどうかは疑わしい。ピアソンのカイ二乗検定のP値が1%未満なのは標本サイズが大きいためである。
⇨ 正しい
② クラメールの連関係数の値が0.1程度なので、標本サイズが大きいが、年代とメディアの間には実質的に有意な関係があると言える。
⇨ クラメールの連関係数が0.1の場合、関連はほとんどないと考えられます。
③ クラメールの連関係数の値が0.5程度なので、年代とメディアの間には中程度の関係があるといえる。
⇨ 今回の問題では、クラメールの連関係数は0.1程度になります。
④ ピアソンのカイ二乗検定のP値は1%未満であるから、年代とメディアの間には強い関係があると言える。
⇨ P値は有意差を測るものであり、関係の強さを測る指標ではありません。
⑤ ピアソンのカイ二乗検定は5%有意ではなく、クラメールの連関係数の値も0.1程度であることから、年代とメディアの間の関係の有無に関する情報を得ることはできない。
⇨ 今回の問題では、ピアソンのカイ二乗検定のP値は1%未満になります。
したがって、選択肢①が正解になります。
問題9-3
年代と最も利用しているメディアの関係に対して主成分分析を行い、その結果のバイプロットを作成した。このグラフの解釈として適切ではないものを答えよ。
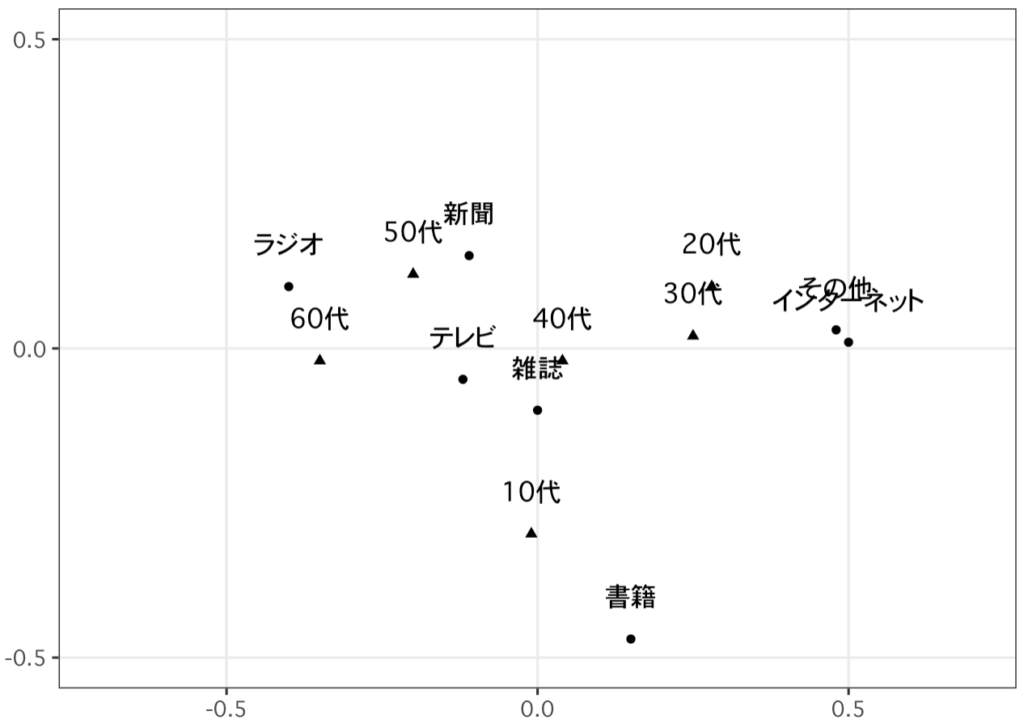
選択肢
① 10代の回答者は20代や30代と比べて、メディアの中でテレビを選択した割合が多い
② 20代, 30代の回答者は他の世代に比べて、メディアの中でインターネットを選択した割合が多い
③ 40代の回答者には、メディアの中で新聞が最も多く選択されている
④ ラジオを選択した回答者の中で50代が占める割合は、書籍を選択した回答者の中で50代が占める割合よりも多い
⑤ 60代の回答者は40代以下に比べて、メディアの中でテレビ, ラジオ, 新聞を選択した割合が多い
答え 選択肢 ③
解説
前提知識
バイプロット
主成分分析を行い、PC1とPC2を配置したグラフ。主成分分析後の値(固有ベクトル)は関連が強い値ほど数値が近くなるため、グラフ上の距離が近いほど関連が強いと判断することができる。
関連の度合いを測定するため、割合の比較を行うことは得意だが、頻度までは分からない
選択肢
選択肢のうち、選択肢③『40代の回答者には、メディアの中で新聞が最も多く選択されている』は頻度の比較をしており、選択肢③以外は割合の比較をしています。
バイプロットでは頻度の比較はできないという特徴があります。
したがって、誤った説明をしているのは選択肢③になります。



