問題8
【設問】
ある学年で100点満点のテストを2回実施し、各テストの点数の累積相対度数分布を作成した。このグラフから読み取れるものとして、適切なものを全て答えよ。
(1回目: 実線 2回目: 点線)
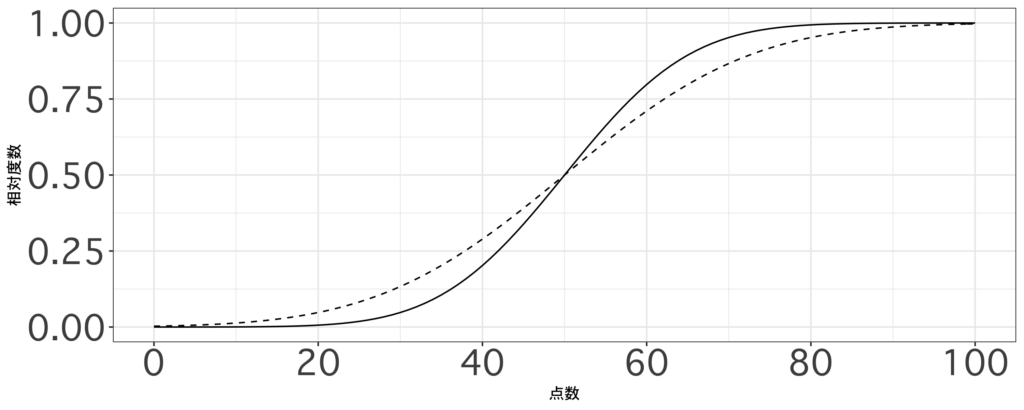
【選択肢】
- 得点が上位の生徒にとって2回目の方が点数が取りにくかった
- 1回目よりも2回目の方が第1四分位数は小さいが第3四分位数は大きい
- 1回目の方が2回目よりも標準偏差が小さい
【答え】2, 3
前提知識
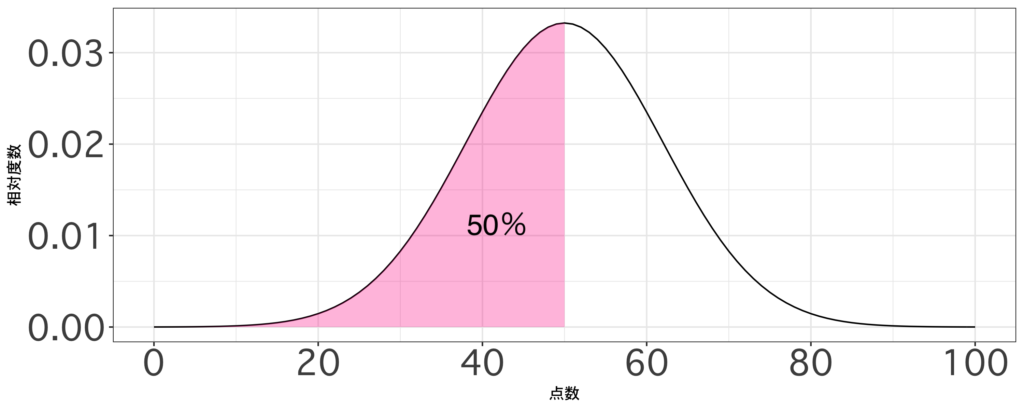
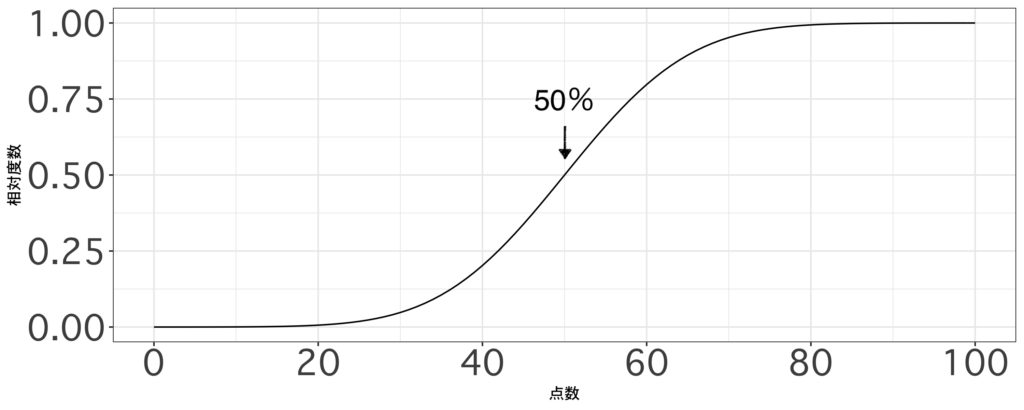
度数分布と累積度数分布
- 度数分布
⇨ 特定の値を取る確率を表した分布 - 累積度数分布
⇨ 特定の値よりも小さい値を取る確率を表した分布
より直感的に説明すると、度数分布の面積と累積度数分布の高さは同じ値を示します。より数学的に説明すると、微分と積分の関係を表したグラフになります。
相対度数
値が出現した回数を度数と呼び、値が出現する確率を相対度数と呼びます。統計学では確率を扱うことが多いため、度数分布よりも相対度数分布が使われることが多いです。
相対度数の計算
\begin{align}
&\text{相対度数}=\frac{\text{度数}}{\text{度数の合計}} \\
\end{align}
解説
問題文では累積相対度数分布が示されていますが、相対度数分布の方が解釈が容易になるため、まずはグラフを変換します。元のグラフは50点を中心に点対象であり、1回目のテスト(実線)の方が傾きが大きいため、変換後のグラフは以下のようになります。
(1回目: 実線 2回目: 転線)
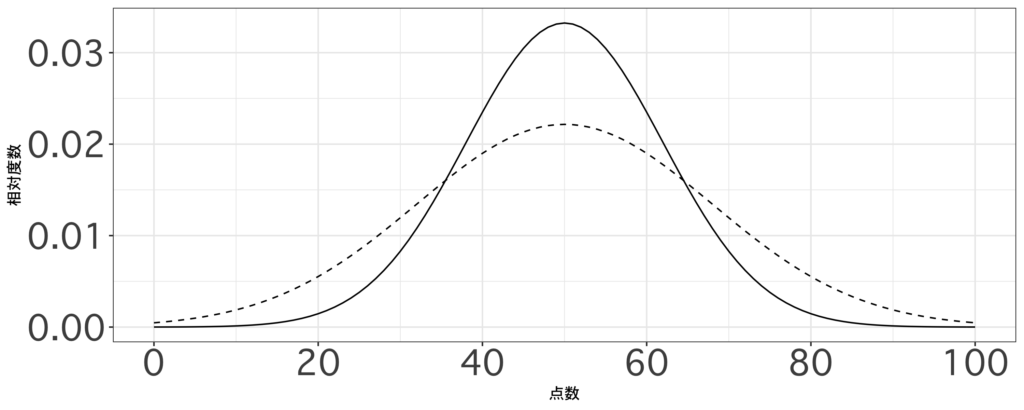
ここから、どちらも平均が50点、2回目の方が標準偏差が大きいことが分かります。
選択肢
- 得点が上位の生徒にとって、2回目(点線)の方が点数が取りにくかった
⇨ 誤り(2回目の方が標準偏差が大きいため、成績上位者は高得点が取りやすい) - 1回目(実線)よりも2回目(点線)の方が、第1四分位数は小さいが第3四分位数は大きい
⇨ 正しい(2回目の方が標準偏差が大きいため、四分位範囲は大きくなる) - 1回目(実線)の方が2回目(点線)よりも標準偏差が小さい
⇨ 正しい(1回目の方が標準偏差が小さい)



