諸注意
- 問題本文は公式サイトまたは公式問題集を参照してください
- 統計検定2級に合格している方を想定して解説していきます
問題9-1&問題9-2
Oリングの破損の有無と外気温の関係を調べるため、外気温を説明変数に持つロジスティック回帰モデルを利用してOリングの破損の有無を推定する。なお、スペースシャトルの打ち上げ回数を\(i=1,2,…,23\)、外気温を\(x_i\)、Oリングの破損の有無を\(y_i\)(1が破損あり、0が破損なし)で表す。この時、下記の(ア)と(イ)に当てはまる選択肢を答えよ。
\(y_i\)は互いに独立な確率変数\(Y_i\)の実現値であり、\(Y_i\)は(ア)に従う。\(\pi_i(0<\pi_i<1)\)について構造式(イ)を仮定する。
(ア)に当てはまる選択肢
① ベルヌーイ分布\(B(1,\pi_i)\) ② 二項分布\(B(23,\pi_i)\) ③ ポアソン分布 ④ 正規分布
(イ)に当てはまる選択肢
① \(log\frac{\pi_i}{1-\pi_i}=a+bx_i\) ② \(\frac{exp(\pi_i)}{1+exp(\pi_i)}=a+bx_i\) ③ \(log\pi_i=a+bx_i\) ④ \(\pi_i=a+bx_i\)
答え (ア)① ベルヌーイ分布 (イ)① \(log\frac{\pi_i}{1-\pi_i}=a+bx_i\)
解説
前提知識
ロジスティック回帰とは、リンク関数にロジット関数を持つ判別手法です。
- 式1-1:ロジット関数
⇨ 対数オッズを用いたモデル
⇨ 成功確率\(\pi_i\)から回帰モデルを求めることができる - 式1-2:ロジスティック関数
⇨ ロジット関数の逆関数
⇨ 回帰モデルから成功確率を求めることができる
式1
\begin{align}
& log\frac{\pi_i}{1-\pi_i}=a+bx_i &(1) \\
& \frac{exp(a+bx_i)}{1+exp(a+bx_i)}=\pi_i &(2) \\
\end{align}
破損の有無を表す確率分布
問題文より、Oリングの破損の有無\(y_i\)は0か1のどちらかの値を取ります。確率変数が0か1のどちらかを取る確率分布はベルヌーイ分布になります。
したがって、(ア)に当てはまる選択肢はベルヌーイ分布\(B(1,\pi_i)\)(選択肢①)になります。
構造式
問題文より、ロジスティック回帰モデルを仮定しているため、リンク関数はロジット関数になります。選択肢と対応する関数名は以下の通りです。
- \(log\frac{\pi_i}{1-\pi_i}=a+bx_i\)
⇨ ロジット関数 - \(\frac{exp(\pi_i)}{1+exp(\pi_i)}=a+bx_i\)
⇨ ロジスティック関数もどき(\(\pi_i\)と\(a+bx_i\)が逆) - \(log\pi_i=a+bx_i\)
⇨ 対数関数 - \(\pi_i=a+bx_i\)
⇨ 恒等関数
したがって、(イ)に当てはまる選択肢は\(log\frac{\pi_i}{1-\pi_i}=a+bx_i\)(選択肢①)が正解になります。
問題9-3
過去23回の打ち上げデータとロジスティック回帰の結果が以下の通りであった。なお、Tempは外気温, TDはOリングの破損の有無を表す。この時、Oリングの破損確率\(\pi_i\)が0.5となる外気温は何度か答えよ。


選択肢
① 14.9°F ② 24.3°F ③ 54.9°F ④ 64.8°F ⑤ 71.7°F
答え ④ 64.8°F
解説
R言語の見方
Call: glm(formula = df$TD ~ df$Temp, family = binomial(link = "logit"))では、非説明変数にOリングの破損の有無(df$TD), 説明変数に外気温(df$Temp)を用いたロジスティック回帰を指定しています。
その結果、Estimateの(Intercept)が15.0429, df$Tempが-0.2322となっています。これは切片aの推定値が15.0429であり、回帰係数b(傾き)が-0.2322であることを表しています。
外気温の計算
問題文より、Oリングの破損確率\(\pi_i\)が0.5になるため、ロジット関数に値を代入して外気温\(x_i\)を計算します。
式2
\begin{align}
log\frac{\pi_i}{1-\pi_i} &= a+bx_i \\
log\frac{0.5}{1-0.5} &= 15.0429 – 0.2322 x_i \\
0 &= 15.0429 – 0.2322 x_i \\
x_i &= \frac{15.0429}{0.2322} = 64.8 \\
\end{align}
したがって、外気温は64.8°F(選択肢④)になります。
問題9-4
問題9-3と同じロジスティック回帰に従う。外気温が31°Fの時、Oリングの破損確率\(\pi_i\)の推定値を答えよ。
選択肢
① 0.0028 ② 0.1589 ③ 0.5820 ④ 0.8979 ⑤ 0.9996
答え ⑤ 0.9996
解説
破損確率の計算
確率の計算はロジスティック関数の得意領域になるため、式1-2(ロジスティック関数)に値を代入してOリングの破損確率\(\pi_i\)を計算します。
式3
\begin{align}
\pi_i &= \frac{exp(a+bx_i)}{1+exp(a+bx_i)} \\
&= \frac{exp(15.0429-0.2322*31)}{(1 + exp(15.0429-0.232231))} \\
&= \frac{exp(7.84)}{(1 + exp(7.84))} \\
&= \frac{2540}{(1 + 2540)} \\
&= 0.9996 \\
\end{align}
したがって、Oリングの破損確率\(\pi_i\)は0.9996(選択肢⑤)になります。
余談
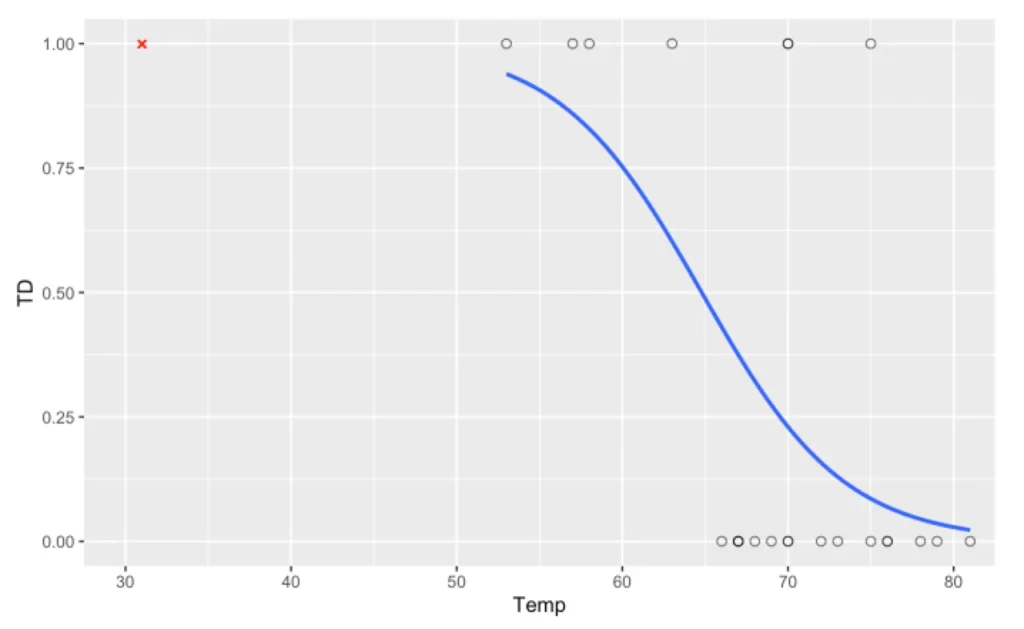
本問のデータをプロットすると、以下のようになります。このように教師データ(23件のデータ)から大きく外れた値を推定することを外挿(または補外)と呼びます。
外挿は的外れな結果を返すこともあるため、推定する際は注意が必要になります。
- 白丸: これまでの23件のデータ
- 赤ばつ: 31°Fのデータ