諸注意
- 問題本文は公式サイトまたは公式問題集を参照してください
- 統計検定2級の資格を持つ方を前提に解説していきます
問題5-1
ある地域では、兄の身長X, 弟の身長Yは2変量正規分布に従う。XとYの期待値はそれぞれ140cmと130cm、標準偏差はいずれも15cm、相関係数が0.6であった。
兄の身長が150cmである時、弟の身長の期待値を答えよ。
① 136cm
② 138cm
③ 140cm
④ 142cm
⑤ 144cm
答え 選択肢 ①
解説
前提知識
2変量正規分布
2つの確率変数が正規分布に従い、これらの間に線形の相関関係が存在する確率分布。本問では以下の2変量正規分布が題材になっています。
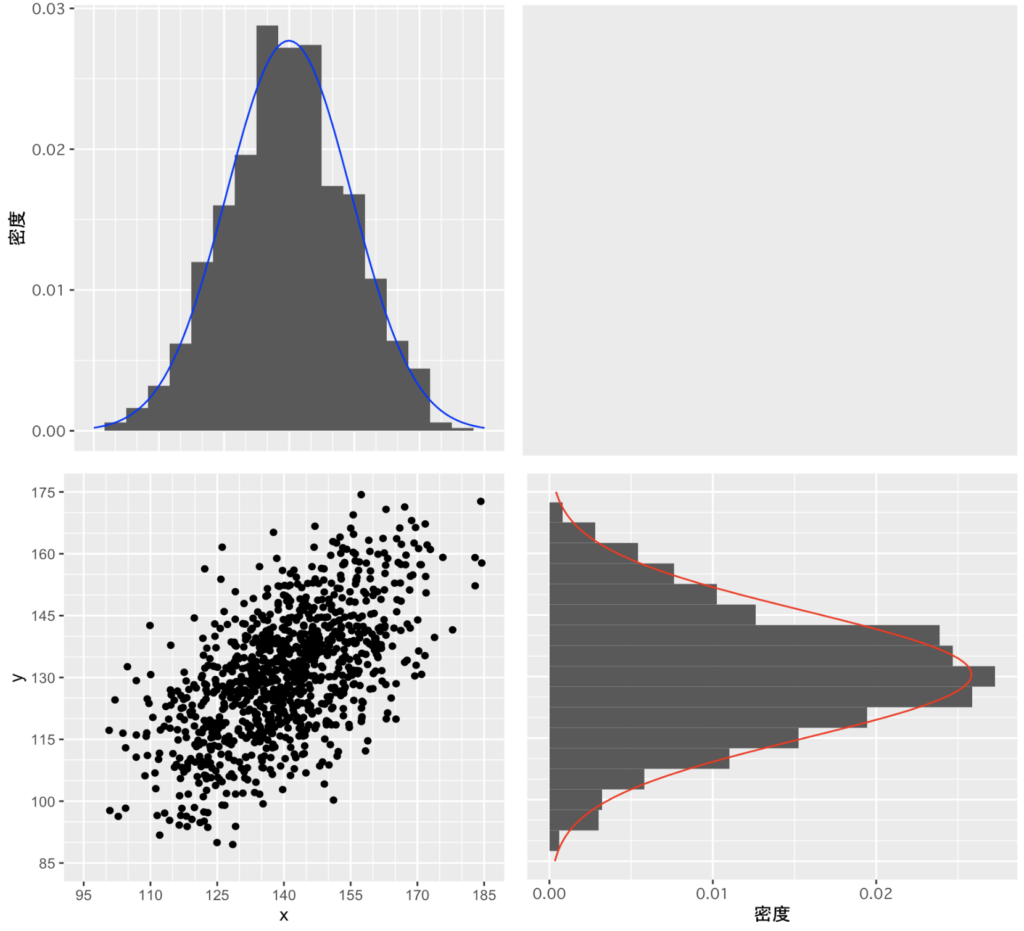
相関係数が変化すると確率変数XとYの確率分布は変化せず、散布図が変化します。以下の散布図は、相関係数が(1.0, 0.8, 0.5, 0.2, 0, -0.2, -0.5, -0.8, -1.0)の散布図を表します。

緑色の線は最小二乗法の結果を表します。
確率変数YをXの線形関数と仮定した時、最小二乗法による推定値は\(\hat{Y}=aX+b\)になります。ここで傾きaはXとYの共分散をXの分散で割った値になります。
詳しくは最小二乗法の解説が必要になるため割愛しますが、Xの変化がYに与える影響の度合い(XとYの共分散)をXの1単位に変換した(Xの分散で割った)と認識してください。
式1
\begin{align}
a = \frac{Cov(X, Y)}{\sigma_x^2} \\
\end{align}
相関係数・共分散・分散の関係は以下の通りです。
式2
\begin{align}
\rho_{xy} &= \frac{Cov(X, Y)}{\sigma_x \cdot \sigma_y} \\
\end{align}
ここから傾きaは相関係数と標準偏差を用いて以下の通り表せます。
式3
\begin{align}
\rho_{xy} \frac{\sigma_y}{\sigma_x} &= \frac{Cov(X, Y)}{\sigma_x^2} \\
\end{align}
次に、偏回帰係数(確率変数Yの条件付き期待値\(E[Y|X=x]\))を求めます。
式3より、確率変数XとYの標準偏差が等しい時、傾きは相関係数\(\rho_{xy}\)と等しくなります。Yの平均が\(\mu_y\)になり、Xが\(\mu_x\)から離れるほど傾き\(\rho_{xy}\)の影響を受ける式を考えます。
式4
\begin{align}
E[Y | X = x] = \mu_y + \rho_{xy} \frac{\sigma_y}{\sigma_x} (x-\mu_x) \\
\end{align}
偏回帰係数
式4より、兄の身長が150cmである時の弟の身長の期待値を求めます。
- 兄の身長の期待値: \(E[X] = 140\)
- 弟の身長の期待値: \(E[Y] = 130\)
- 分散(兄弟共通): \(V[X] = V[Y] = 15^2\)
- 相関係数: \(\rho = 0.6\)
式5
\begin{align}
E[Y | X = 150] &= 130 + 0.6 \cdot \frac{15}{15} \cdot (150-140) = 136
\end{align}
したがって、弟の身長の期待値は136cmになります。
問題5-2
ランダムに選ばれた弟の身長が115cm以上である確率を答えよ。
① 0.68
② 0.72
③ 0.76
④ 0.80
⑤ 0.84
答え 選択肢 ⑤
解説
前提知識
正規分布
正規分布は平均値から標準偏差だけ離れた時に含まれる値の割合が定まっています。以下のグラフは、各範囲に含まれる値の割合を示しています。
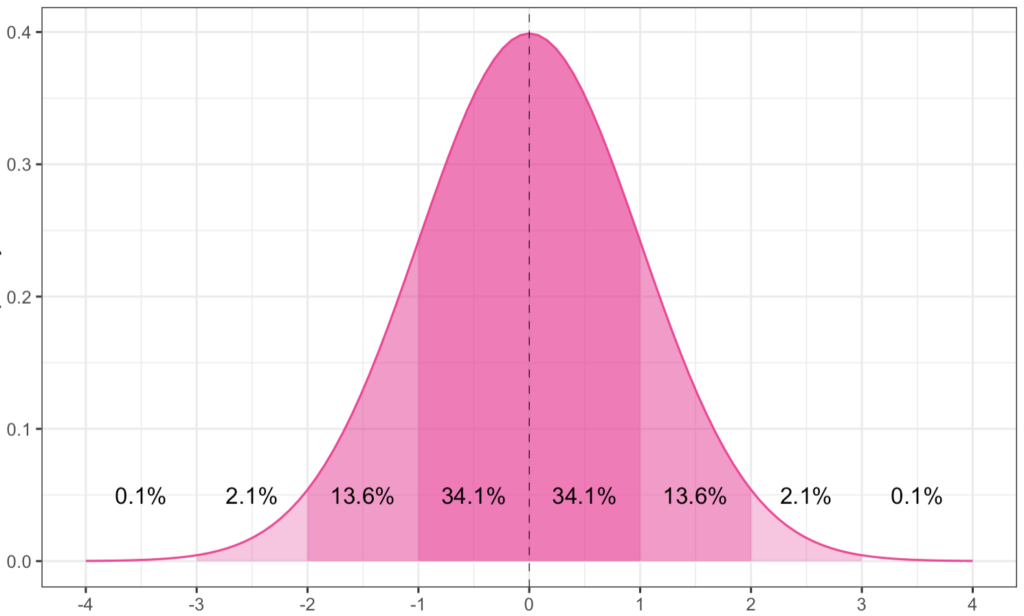
正規分布
問題文より、平均\(E[Y]\)が130cm, 分散V[Y]が15cmである時、弟の身長が115cm以上である確率を尋ねています。ここから、以下の式で求めます。
式6
\begin{align}
P(115 < Y) = 0.341 + 0.341 + 0.136 + 0.021 + 0.001 = 0.84
\end{align}
したがって、弟の身長が115cm以上になる確率は84%になります。
問題5-3
ランダムに選ばれた兄の身長が弟の身長よりも20cm以上高い確率を答えよ。
① 0.23
② 0.25
③ 0.27
④ 0.29
⑤ 0.31
答え 選択肢 ①
解説
前提知識
確率分布
正規分布を含む確率分布は以下の性質を持ちます。
- 式7-1: 期待値の線形性
⇨ 『確率変数の和の期待値』と『確率変数の期待値の和』が等しい - 式7-2: 分散の加法性(2変量が独立である時のみ)
⇨ 『確率変数の和の分散』と『確率変数の分散の和』が等しい - 式7-3: 分散の合成(2変量が共分散を持つ時のみ)
⇨ X±Yの分散は、XとYの分散及び共分散を用いて求めることができる
⇨ 共分散が0(独立)の場合は分散の加法性と一致します
式7
\begin{align}
&E[X \pm Y] = E[X] \pm E[Y] & (1) \\
&V[X \pm Y] = V[X] + V[Y] & (2) \\
&V[X \pm Y] = V[X] + V[Y] \pm 2 Cov(X,Y) & (3) \\
\end{align}
分散の合成
\(Z = X-Y\)の時の導出式
式8
\begin{align}
V[Z] &= E[(Z-E[Z])^2] \\
&= E[((X-Y)-E[X-Y])^2] \\
&= E[((X-Y)-(E[X]-E[Y]))^2] \\
&= E[(X-Y-E[X]+E[Y])^2] \\
&= E[(X-E[X]-Y+E[Y])^2] \\
&= E[((X-E[X])-(Y-E[Y]))^2] \\
&= E[(X-E[X])^2-2(X-E[X])(Y-E[Y])+(Y-E[Y])^2] \\
&= E[(X-E[X])^2]-2E[(X-E[X])]E[(Y-E[Y])]+E[(Y-E[Y])^2] \\
&= V[X]-2Cov(X,Y)+V[Y] \\
\end{align}
(\(X-Y\))の合成分布
兄の身長Xが弟の身長Yよりも20cm以上高い確率を求めるため、まずは(X – Y)が従う確率分布を求めます。この時、(X – Y)が従う正規分布の期待値と分散を式7より求めます。
なお、共分散は\(Cov(X, Y) = \rho \sigma_x \sigma_y\))で求めることができます。
式9
\begin{align}
E[X-Y] &= 140 – 130 = 10 \\
V[X-Y] &= 15^2 + 15^2 – 2 \cdot 0.6 \cdot 15 \cdot 15 = 180 \\
\end{align}
標準化
期待値が10cm, 分散が180cmの正規分布に従う場合、(X – Y)が20cmの時のZスコア(標準化した時の標準偏差)は以下の通り求めます。
式10
\begin{align}
\frac{20-10}{\sqrt{180}} = 0.745
\end{align}
Zスコア
Zスコアが0.745以上になる確率は、付表(標準正規分布の上側確率)より23%になります。
したがって、兄の身長が弟の身長より20cm以上高くなる確率は23%になります。


