諸注意
- 問題本文は公式サイトまたは公式問題集を参照してください
- 統計検定2級に合格している方を想定して解説していきます
問題12-1
p次の自己回帰モデルAR(p)は式1で表される。AR(2)モデルが\(a_1=a_2=a(0<a)\)のとき、定常であるためのaに関する必要十分条件を答えよ。なお、AR(2)モデルが定常であることの必要十分条件は式2の方程式の全ての解の絶対値が1より大きくなることである。
式1
\begin{align}
X_t &= c+\sum_{i=1}^pa_iX_{t-i}+\epsilon_t
\end{align}
\(c, a_i\)は実数, \(t\)は整数, \(\epsilon_t\)は互いに独立に\(N(0, \sigma^2)\)に従う実数
式2
\begin{align}
1&-a_1z-a_2z^2=0
\end{align}
答え \(a<0.5\)
解説
二次方程式の計算
定常であるための必要十分条件(式2)が提示されているため、\(a_1=a_2=a(0<a)\)の条件下で解の公式を用いて二次方程式を解きます。
式3
\begin{align}
1-az-az^2 &= 0 \\
az^2+az-1 &= 0 \\
z &= \frac{-a\pm \sqrt{a^2-4a(-1)}}{2a} \\
z &= \frac{-a\pm\sqrt{a^2+4a}}{2a} \\
z &= \frac{-1\pm\sqrt{1+4/a}}{2} \\
\end{align}
次に、解の絶対値が1より大きくなるaの値を求めます。計算は省略しますが、結果は以下の通りになります。
式4
\begin{align}
1 &< \frac{-1+\sqrt{1+4/a}}{2} \longleftarrow a < 0.5 \\
1 &< \frac{-1-\sqrt{1+4/a}}{2} \longleftarrow \text{解なし} \\
-1 &> \frac{-1+\sqrt{1+4/a}}{2} \longleftarrow \text{解なし} \\
-1 &> \frac{-1-\sqrt{1+4/a}}{2} \longleftarrow \text{解なし} \\
\end{align}
したがって、AR(2)モデルが定常であることの必要十分条件は\(a<0.5\)になります。
問題12-2
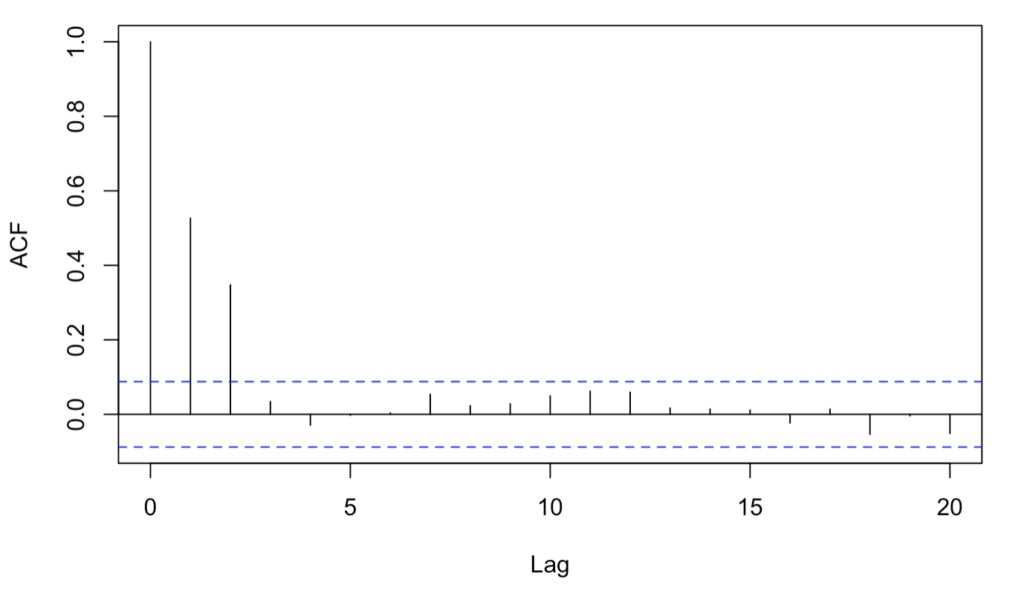
q次の移動平均モデルMA(q)は式6で表される。MA(q)モデルの\(b_i\)の値を全て0.5に設定したとき、以下のコレログラムが生成された。この時、モデルの次数(q)の値を答えよ。また、そのように考えた理由を数式で示せ。なお、青色の点線は無相関であるという帰無仮説下での棄却域を表す。
式6
\begin{align}
X_t &= c+\epsilon_t+\sum_{i=1}^qb_i\epsilon_{t-i} \\
\end{align}
\(c, b_i\)は実数, \(\epsilon_t\)は互いに独立に\(N(0, \sigma^2)\)に従う実数
答え \(q=2\)(根拠は解説参照)
解説
コレログラムと相関係数
コレログラムはX軸がラグ・Y軸が自己相関係数を表しています。本問で提示されたコレログラムから、おおよその相関係数を以下の通り読み取ります。
式7
\begin{align}
&lag0: Cor(X_t, X_t)=1 \\
&lag1: Cor(X_t, X_{t-1})=1/2 \\
&lag2: Cor(X_t, X_{t-2})=1/3 \\
&lag3: Cor(X_t, X_{t-3})=0 \\
\end{align}
詳細は後述しますが、ラグ2まで相関が見られるため、モデルの次数qは2が正解になります。
移動平均モデル
本問におけるMA(2)モデルを展開すると、以下の式の通りになります。なお、相関の計算では定数は無視するため、定数cは省略します。
式8
\begin{align}
&X_t = \color{red}{\epsilon_t}+\color{red}{b_1\epsilon_{t-1}}+\color{red}{b_2\epsilon_{t-2}} \\
&X_{t-1} = \color{red}{\epsilon_{t-1}}+\color{red}{b_1\epsilon_{t-2}}+b_2\epsilon_{t-3} \\
&X_{t-2} = \color{red}{\epsilon_{t-2}}+b_1\epsilon_{t-3}+b_2\epsilon_{t-4} \\
&X_{t-3} = \epsilon_{t-3}+b_1\epsilon_{t-4}+b_2\epsilon_{t-5} \\
\end{align}
赤色表記の箇所は\(X_t\)と重複する\(\epsilon\)を持つ項を示します
本問では\(\epsilon\)がそれぞれ独立であるため、同じ\(\epsilon\)を持たない移動平均Xの自己相関係数は無相関になります。ここからもMA(2)モデルが正解であることが分かります。
自己相関係数の計算
式7の通り、グラフからおおよその自己相関係数を求めることができます。この値を計算によって導くため、まずは\(X_t\)の分散を求めます。
式9
\begin{align}
V[X_t] &= V[\epsilon_t+b_1\epsilon_{t-1}+b_2\epsilon_{t-2}] \\
&= V[\epsilon_t]+V[b_1\epsilon_{t-1}]+V[b_2\epsilon_{t-2}] \\
&= V[\epsilon_t]+b_1^2V[\epsilon_{t-1}]+b_2^2V[\epsilon_{t-2}] \longleftarrow \epsilon \sim N(0, \sigma) \\
&= \sigma^2+b_1^2\sigma^2+b_2^2\sigma^2 \longleftarrow b_1=b_2=0.5 \\
&= \sigma^2+0.5^2\sigma^2+0.5^2\sigma^2 \\
&= 1.5\sigma^2 \\
\end{align}
なお、\(X_{t-1}, X_{t-2}…\) の分散も同じ値になります。
次に、\(X_t\)と\(X_{t-1}\)の共分散を求めます。なお、それぞれの\(\epsilon\)は独立した正規分布に従うため、異なる値同士は無相関になります。
式10
\begin{align}
Cov(X_t, X_{t-1}) &= Cov(\epsilon_t+b_1\epsilon_{t-1}+b_2\epsilon_{t-2}, \epsilon_{t-1}+b_1\epsilon_{t-2}+b_2\epsilon_{t-3}) \\
&= Cov(\epsilon_t\epsilon_{t-1}+…+b_1\epsilon_{t-1}^2+…+b_1b_2\epsilon_{t-2}^2+…) \\
&= Cov(\epsilon_t\epsilon_{t-1})+…+Cov(b_1\epsilon_{t-1}^2)+…+Cov(b_1b_2\epsilon_{t-2}^2)+… \\
&= 0+…+b_1Cov(\epsilon_{t-1}^2)+…+b_1b_2Cov(\epsilon_{t-2}^2)+… \\
&= 0+…+b_1V(\epsilon_{t-1})+…+b_1b_2V(\epsilon_{t-2})+… \\
&= 0+…+b_1\sigma^2+…+b_1b_2\sigma^2+… \\
&= 0+…+0.5\sigma^2+…+0.5^2\sigma^2+… \\
&= 0.75\sigma^2
\end{align}
3点リーダ(…)の箇所は無相関の箇所を表します
最後に、\(X_t\)と\(X_{t-1}\)の相関係数を求めます。
式11
\begin{align}
Cor(X_t,X_{t-1}) &= \frac{Cov(X_t,X_{t-1})}{S[X_t]S[X_{t-1}]} = \frac{0.75\sigma^2}{\sqrt{1.5\sigma^2}\sqrt{1.5\sigma^2}} = \frac{1}{2}
\end{align}
同様に、\((X_t,X_{t-2})\)と\((X_t,X_{t-3})\)の相関係数を求めます。
式12
\begin{align}
Cov(X_t, X_{t-2}) &= Cov(\epsilon_t+b_1\epsilon_{t-1}+b_2\epsilon_{t-2}, \epsilon_{t-2}+b_1\epsilon_{t-3}+b_2\epsilon_{t-4}) \\
&= Cov(b_2\epsilon_{t-2}^2) \\
&= 0.5\sigma^2 \\
\\
Cor(X_t,X_{t-2}) &= \frac{0.5\sigma^2}{\sqrt{1.5\sigma^2}\sqrt{1.5\sigma^2}} = \frac{1}{3} \\
\end{align}
式13
\begin{align}
Cov(X_t, X_{t-3}) &= Cov(\epsilon_t+b_1\epsilon_{t-1}+b_2\epsilon_{t-2}, \epsilon_{t-3}+b_1\epsilon_{t-4}+b_2\epsilon_{t-5}) = 0 \\
Cor(X_t,X_{t-2}) &= \frac{0.5\sigma^2}{\sqrt{1.5\sigma^2}\sqrt{1.5\sigma^2}} = \frac{1}{3} \\
\end{align}
式11, 12, 13の結果は、問題文で提示されたコレログラムと一致しています。
したがって、MA(2)モデルが採用されていると考えられます。



